Rankings, rankings, rankings… ¡Están por todos lados! La Real Academia Española define un ranking como una clasificación de mayor a menor, útil para establecer criterios de valoración. Los rankings se utilizan continuamente para comparar universidades entre sí, como el internacional Times Higher Education (THE) o nuestro nacional U-Ranking de universidades españolas.
En administración de empresas y negocios, monitores de reputación corporativa como Merco o Great Place to Work elaboran listas de las mejores empresas en las que trabajar. Sin embargo, no hace falta referenciar ámbitos académicos y profesionales para ver la utilidad de los rankings. Concursos televisivos como Eurovisión o competiciones deportivas como la Fórmula 1 se nutren de rankings para clasificar individuos a través de metodologías muy concretas, para así determinar el orden de ganadores.
Sistemas de puntuación clásicos, y sus limitaciones
La forma más típica de establecer un ranking global entre varios criterios particulares consiste en otorgar una puntuación numérica a cada individuo y en cada criterio, para después sumarlos y compararlos globalmente. De forma general, este método está adaptado en varios de los ejemplos que hemos mencionado antes.
En el caso de Eurovisión, las clasificaciones están conformadas por los votos del jurado y del televoto. Para los votos del jurado profesional, cada país participante proporciona 5 expertos musicales que otorgan 12 puntos a su canción favorita, 10 puntos a su segunda canción favorita, y puntuaciones desde el 8 hasta el 1 para las siguientes ocho mejores. Los televotos otorgan la misma distribución de puntos, por cada país participante, más una categoría adicional de país que representa al resto del mundo. El ganador queda determinado por quién obtenga una mayor suma entre ambas categorías.

En la Fórmula 1, podemos considerar cada gran premio como un criterio independiente de la clasificación general. Si el gran premio se corre como carrera convencional, el primer piloto recibe 25 puntos, 18 van para el segundo, 15 para el tercero, 12 para el cuarto, 10 para el quinto, 8 para el sexto, 6 para el séptimo, 4 para el octavo, 2 para el noveno, 1 para el décimo, y un punto adicional para quien corra la vuelta más rápida. Si el gran premio se corre como sprint, el primer piloto recibe 8 puntos, el segundo recibe 7 y así sucesivamente hasta llegar al octavo piloto, que recibe 1 punto. La clasificación general se obtiene como la suma de las puntuaciones de todos los pilotos.
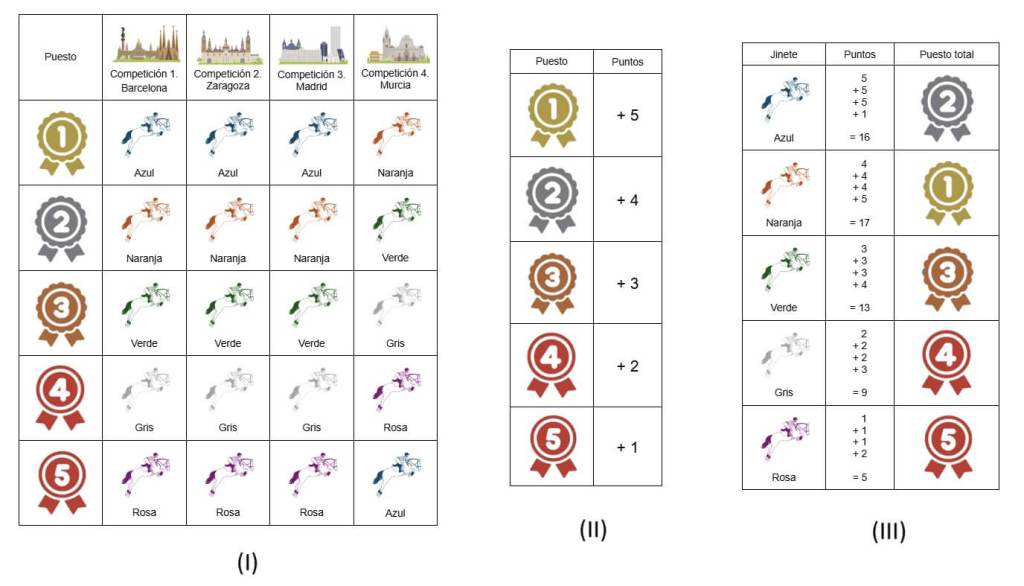
Si bien resulta fácil atribuir puntuaciones numéricas a determinados escalones en rankings para luego sumarlos y obtener clasificaciones más generales, esta simplificación a veces tiene sus limitaciones. Pongamos como ejemplo una liga de equitación entre unos jinetes azul, naranja, verde, gris y rosa, según (I). Esta liga de equitación tiene 4 competiciones diferentes, una en Barcelona, otra en Zaragoza, la tercera en Madrid y la última en Murcia. En cada una de estas competiciones, otorgamos 5 puntos al primer jinete, 4 al segundo y así sucesivamente hasta llegar al último, que recibe 1 punto, tal y como está en (II). Si siguiéramos esta forma de puntuar, el jinete naranja acabaría el primero, segundo estaría el azul, tercero el verde, cuarto el gris y quinto el rosa, según (III). Si bien el primer jinete resultante es el naranja, en 3 de las 4 competiciones el jinete azul es el primero: precisamente el pésimo resultado en la cuarta competición es lo que le arrastra a acabar por detrás del jinete naranja, en la clasificación general. Esta cuarta competición podría considerarse como una especie de anómalo. Si se celebrase una quinta carrera y tuviéramos que predecir su resultado, seguramente colocaríamos al jinete azul como mejor que el naranja.
De esta manera, ¿existe alguna otra forma de clasificar elementos que no dependa en atribuir puntuaciones a posiciones en concreto? O sea, partiendo de la misma tabla de competiciones en (I), ¿podría el jinete azul superar al jinete naranja en alguna clasificación global? La respuesta a ambas es que sí, y que el quid de la cuestión reside en cómo construir esta clasificación global. Para ello, la Investigación Operativa (IO), rama dentro de las Matemáticas Aplicadas, nos brinda un problema de optimización para el agregado de rankings de forma más representativa y sin recurrir a puntuaciones numéricas: el Linear Ordering Problem.
El enfoque alternativo del Linear Ordering Problem
El Linear Ordering Problem (LOP), que podría traducirse como Problema de Ordenamiento Lineal, fue descrito por primera vez en 1958. Se considera un problema de optimización combinatoria de tipo NP-duro, lo que refleja su dificultad matemática y computacional para resolver instancias grandes del problema.
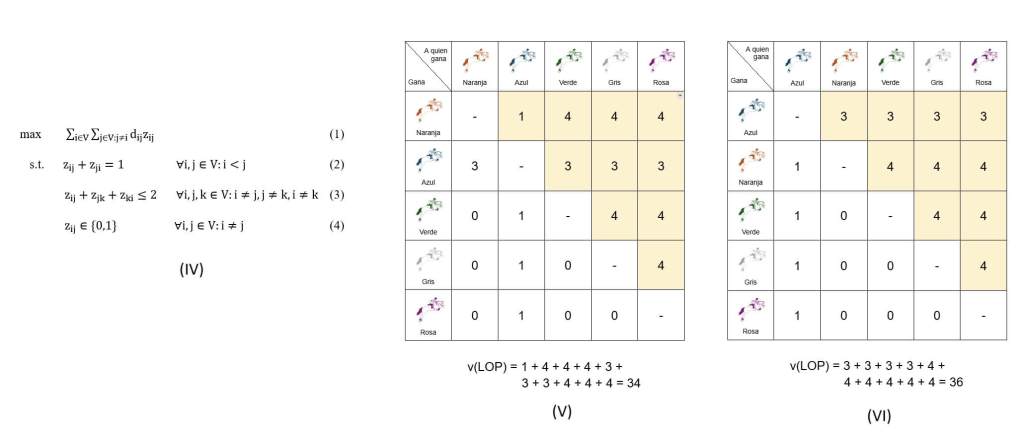
En términos técnicos [1], el problema busca la permutación de filas y columnas de una matriz cuadrada positiva que maximice la suma de su diagonal superior, modelado a través de (IV). Consideramos una matriz de preferencia D formada por elementos dij, que representan el número de veces que un jinete i supera a otro jinete j. La función objetivo (1) representa esa suma de la diagonal superior que queremos maximizar. La restricción (2) plantea que, en nuestra clasificación global resultante, o el jinete i gana al jinete j o el jinete j gana al jinete i, pero no ambos simultáneamente. La restricción (3) desactiva los casos prohibidos; si el jinete i precede al jinete j y el jinete j precede al jinete k, entonces el jinete k no puede preceder al jinete i. Finalmente, la expresión (4) restringe la variable de decisión al dominio binario.
La explicación en términos no técnicos resulta más sencilla e intuitiva. El mecanismo de clasificación global consiste en comparar las posiciones de cada jinete con respecto de los demás, una a una, para todas las competiciones. Una vez contemos cuántas veces cada jinete ha ganado a cada uno de los demás, los ponemos en una matriz según el orden que queramos. El problema de optimización consiste en obtener el orden más representativo, con el que la matriz obtenga la mayor suma de los elementos por encima de su diagonal.
Veámoslo con nuestro ejemplo, suponiendo la clasificación global según el sistema de puntuación clásico: jinete naranja, azul, verde, gris y rosa. Este orden está representado en la matriz de (V). La primera fila representa cuántas veces el jinete naranja gana a cada jinete: ninguna a sí mismo, 1 vez al azul, y 4 veces a los jinetes verde, gris y rosa. La segunda fila nos dice que el jinete azul gana a cada jinete unas 3 veces, y así sucesivamente con el resto de jinetes. Sumando todos los elementos en la diagonal superior de la matriz, en amarillo, se obtiene un valor del LOP, v (LOP), de 34.
¿Puede haber un valor más elevado, más óptimo, que 34? Precisamente, si probamos el orden en el que el jinete azul es el primero, el jinete naranja el segundo, y el resto sin cambiar, obtendríamos un v (LOP) de 36, según (VI). Este valor es el óptimo del problema, por lo que sería la clasificación global más representativa y justa que nos da el LOP. Vemos que, partiendo de la misma tabla de clasificaciones, el LOP nos da un ganador diferente al de un sistema de puntuación clásico.
Otras líneas de investigación en rankings
Si bien el ejemplo ilustra una aplicación básica sobre el LOP, su investigación va mucho más allá. Dada la complejidad matemática del LOP en problemas grandes, algunos autores desarrollan algoritmos heurísticos que puedan hallar soluciones lo suficientemente buenas en un tiempo razonable. Estos heurísticos sustituyen el modelo exacto de (IV) por otros métodos, con algunos inspirados en la evolución darwiniana de las especies [2] o en la comunicación con feromonas entre hormigas en una colonia [3].
Otros autores prefieren darle una vuelta al LOP, extendiendo el modelo para más usos. Cuando los elementos individuales pueden agruparse, como equipos formados por atletas o partidos formados por políticos, el LOP pasa a ser un LOP por clusters [4]. Cuando cada elemento individual tiene una importancia relativa asignada, tendríamos el LOP por pesos [5]. Cuando se asigna la importancia relativa al criterio (y no al cliente) específico, se tendría el LOP por pesos de rankings [6], y… ¡La lista sigue!
En cualquier caso, hemos visto que los sistemas de puntuación tradicionales en rankings no siempre son los más representativos, y cómo instrumentos matemáticos más avanzados como el LOP pueden ofrecer clasificaciones generales más adecuadas. Una vez más, las matemáticas nos ayudan a modelizar (prácticamente) todo lo que nos rodea, favoreciendo una toma de decisiones más informada y eficiente.
Referencias
- [1] Martí, R., & Reinelt, G. (2011). The linear ordering problem: exact and heuristic methods in combinatorial optimization(Vol. 175). Springer Science & Business Media.
- [2] Mishra, N. K., & Singh, P. K. (2022). Linear ordering problem based classifier chain using genetic algorithm for multi-label classification. Applied Soft Computing, 117, 108395.
- [3] Chira, C., Pintea, C. M., Crisan, G. C., & Dumitrescu, D. (2009, July). Solving the linear ordering problem using ant models. In Proceedings of the 11th Annual conference on Genetic and evolutionary computation (pp. 1803-1804).
- [4] Alcaraz, J., Landete, M., Monge, J.F. (2022). Rank Aggregation: Models and Algorithms. In: Salhi, S., Boylan, J. (eds) The Palgrave Handbook of Operations Research . Palgrave Macmillan, Cham. doi: 10.1007/978-3-030-96935-6_5
- [5] Hautz, J., Hungerländer, P., Lechner, T., Maier, K., & Rescher, P. (2020). The weighted linear ordering problem. In Operations Research Proceedings 2019: Selected Papers of the Annual International Conference of the German Operations Research Society (GOR), Dresden, Germany, September 4-6, 2019 (pp. 223-229). Springer International Publishing.
- [6] Vieira, M. V. (2024). A linear ordering problem with weighted rank. Journal of Combinatorial Optimization, 47(2), 13.

Íñigo Martín Melero
Graduado en Ingeniería Mecánica. Máster en Ingeniería Industrial.


Mercedes Landete Ruiz
Licenciada en Matemáticas, Diplomada en Estadística, Doctora en Matemáticas


