Un reciente video viral mostró un experimento con dos ruedas de distinto tamaño rodando sobre una mesa, dejando perplejos a miles de espectadores. En la demostración, cada rueda recorre por separado una distancia acorde a su circunferencia. La grande avanza más que la pequeña. Sin embargo, al fijar la rueda pequeña dentro de la grande y hacerlas rodar juntas, ambas cubren exactamente la misma distancia en una vuelta. Esta aparente contradicción desconcierta a primera vista: ¿cómo puede la rueda pequeña, de menor circunferencia, desplazarse tanto como la grande sin “estirarse”? La situación desafía la intuición y evoca un antiguo enigma, planteando un problema que parece carecer de explicación sencilla.
Lo que presenciaron los usuarios de redes sociales no es un truco de cámara, sino la famosa paradoja de la rueda de Aristóteles, un rompecabezas descrito hace más de dos mil años y que sigue generando asombro. En la obra Mecánica atribuida a Aristóteles, ya se discutía este curioso caso de las dos ruedas concéntricas. Matemáticos y filósofos a lo largo de la historia –desde la Grecia clásica hasta la era moderna– han analizado el fenómeno, dándonos pistas para resolver el misterio. De hecho, al describir el caso se señala que la rueda grande recorre su circunferencia completa mientras la rueda menor, al ir acoplada, recorre más distancia que su propia circunferencia, de modo que “aquí tenemos una flagrante paradoja”. ¿Dónde está el truco entonces? Las páginas de la historia de la ciencia encierran la respuesta, mezclando sutilezas de geometría, rozamiento e incluso la naturaleza del infinito.
¿En qué consiste la paradoja?
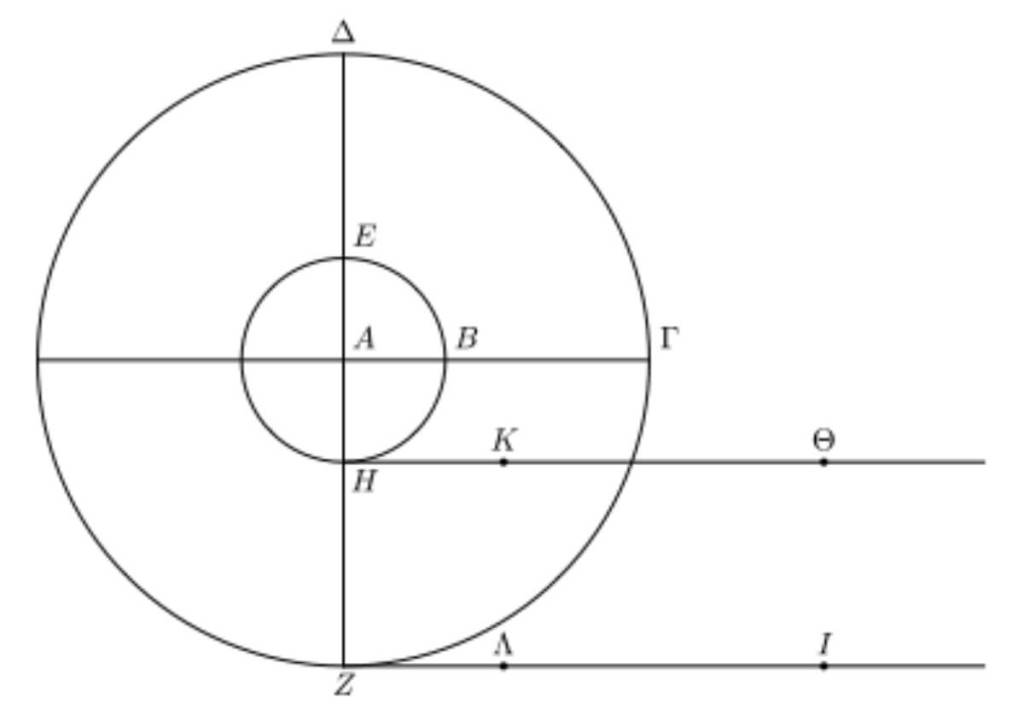
La paradoja de Aristóteles se presenta con una rueda ideal representada por dos circunferencias concéntricas: una externa grande y otra interna más pequeña, unidas rígidamente por el mismo eje. Para entender este artículo es imprescindible que veas el vídeo del que hablamos.
Ahora, imaginemos que la rueda grande está en contacto con una superficie horizontal (como una carretera) y que rueda sin resbalar sobre ella. Al completar una vuelta, el borde exterior ha recorrido una distancia igual a la circunferencia de la rueda grande, como era de esperarse. Pero, al estar la rueda pequeña unida a la grande, su centro se mueve conjuntamente, de modo que la rueda interna también da una vuelta completa. Si pensamos en la rueda pequeña rodando por sí sola, esperaríamos que avanzara solo lo equivalente a su menor circunferencia. Sorprendentemente, al estar acoplada, la circunferencia interna termina cubriendo la misma distancia lineal que la externa, superando la longitud de su propia circunferencia. Esta discrepancia –una rueda pequeña “avanzando de más”– es el meollo de la paradoja. A simple vista, las matemáticas básicas parecen contradecirse: ¿cómo pueden dos circunferencias de tamaños distintos sin deformarse cubrir el mismo recorrido con una sola rotación?
Un enigma desde la Antigüedad
Para visualizar el enigma, imaginemos marcar un punto en el borde de cada rueda al inicio del experimento. Al rodar juntas una vuelta completa, el punto del perímetro externo habrá tocado sucesivamente cada porción del suelo hasta avanzar 2πR (siendo R el radio de la rueda grande). El punto marcado en la rueda menor no toca el suelo (pues la rueda pequeña está suspendida dentro de la grande), pero al girar solidariamente también habrá dado una vuelta completa respecto al eje común. Geométricamente, a cada posición del punto externo corresponde una posición del punto interno alineada radialmente; de hecho, existe una biyección uno a uno entre los puntos de la circunferencia grande y los de la pequeña durante la rotación. Esto sugeriría que la rueda pequeña “debería” recorrer simultáneamente 2πr (con r su radio) y 2πR, lo cual es imposible si 2πr < 2πR. La paradoja nace precisamente de aplicar indiscriminadamente reglas geométricas ideales: asumimos que rodar sin deslizar implica lo mismo para ambas ruedas, llevando a un resultado que desafía la lógica convencional. No es de extrañar que este acertijo intrigara a grandes mentes durante siglos.

Galileo y los espacios “vacíos” en la rueda
En el siglo XVII, Galileo Galilei aportó una idea brillante para desentrañar la paradoja, conectándola con su defensa del atomismo. En su obra Dos nuevas ciencias (1638), Galileo propuso reemplazar las circunferencias por polígonos –concretamente, imaginó dos hexágonos concéntricos en lugar de círculos– para simplificar el análisis. Al hacer “rodar” un hexágono grande sobre una superficie, es fácil ver que cada lado traza una línea recta al contacto con el suelo, mientras el hexágono pequeño, al ir montado, no siempre tiene un lado apoyado. Cada vez que el hexágono externo gira sobre una cara nueva, el hexágono interior queda brevemente suspendido en el aire, “saltando” un pequeño trecho del recorrido. Galileo notó que el hexágono interno deja una huella discontinua: no toca el suelo en ciertas etapas, creando espacios vacíos en su trayectoria. Al aumentar el número de lados del polígono –pasando de un hexágono a polígonos con más y más caras– la rodadura se va asemejando cada vez más a la de un círculo. Pero crucialmente, esos pequeños saltos del polígono interior siguen existiendo, aunque cada vez más pequeños. En el límite de infinitos lados (es decir, el círculo perfecto), el hexágono interior se convierte en la circunferencia interna, y los saltos se transforman en “vacíos” infinitesimales distribuidos a lo largo del camino.
Galileo imaginó sustituir las circunferencias por hexágonos concéntricos para analizar la paradoja. En esta ilustración, el hexágono exterior (azul) rueda sin deslizar, dejando un trazo continuo en el suelo, mientras que el hexágono interior (rojo) es arrastrado y no siempre está en contacto, dejando solo trazos discontinuos (líneas rojas) con espacios vacíos entre ellos.
El ingenioso enfoque de Galileo reveló la solución conceptual: la rueda pequeña, al estar fija dentro de la grande, no recorre cada punto del trayecto de forma continua. Algunas porciones de lo que sería su recorrido “ideal” simplemente no se manifiestan como contacto real con el suelo. En términos de Galileo, la rueda contiene puntos de apoyo y vacíos intercalados. Al describir el caso con un polígono de mil lados, señaló que el polígono menor avanza casi lo mismo que el mayor, pero su camino se compone de “mil pequeñas partículas... con mil pequeños espacios vacíos interpuestos”. Traducido al lenguaje del círculo, esto quiere decir que la circunferencia interna resbala en ciertos instantes en lugar de rodar puramente. El resultado es que ambas ruedas acopladas avanzan igual distancia, pero la rueda pequeña lo hace combinando rodadura y deslizamiento. Galileo concluyó que, si la materia fuese discontinua (hecha de “átomos” indivisibles), esos espacios infinitesimales explicarían por qué la rueda interna no traza una línea continua equivalente a su circunferencia. En sus propias palabras, los “vacíos interpuestos no se cuantifican, pero son infinitos”, de modo que el recorrido del círculo menor incluye una infinidad de minúsculas interrupciones. Esta idea anticipaba nociones de la física atómica y de las matemáticas del infinito, mostrando cómo la paradoja rozaba cuestiones profundas sobre la estructura continua de la materia y el espacio.
Rodar versus deslizar: la explicación física
Desde una perspectiva física moderna, la paradoja se aclara distinguiendo entre rodar y deslizar. La rueda exterior, al estar en contacto con el suelo, rueda sin resbalar; cada punto de su perímetro toca momentáneamente el suelo y se levanta, de modo que no hay deslizamiento neto. En cambio, la rueda interior no toca el suelo en absoluto: gira solidariamente, pero “flota” arrastrada por la estructura externa. Esto significa que su movimiento relativo al suelo no es un rodamiento puro, sino un movimiento combinado. Si imagináramos que el círculo pequeño tuviera su propio camino por dentro de la rueda grande, veríamos que patina sobre ese camino. Dicho de otro modo, la rueda pequeña desliza respecto al suelo mientras es llevada por la grande, aunque no podamos verlo directamente porque está suspendida en el aire.
Un experimento mental puede ayudar: pensemos en pegar una moneda pequeña (digamos de 10 céntimos) al interior de una moneda grande (de 10 céntimos). Al rodar el conjunto sobre una mesa apoyado en la moneda grande, la moneda pequeña gira en el aire. Si pudiéramos colocar otra superficie tocando la moneda pequeña por su lado interno, notaríamos que esta moneda menor resbala sobre esa superficie en lugar de rodar plenamente. De hecho, cuando el sistema avanza una vuelta completa de la rueda grande, el centro común de las monedas se trasladó la misma distancia que la moneda grande recorrió (su circunferencia). La moneda pequeña giró el mismo ángulo, pero como no tuvo contacto con el suelo, su rotación no se tradujo en desplazamiento lineal propio. Es arrastrada, no “camina” sobre el suelo punto por punto. Este deslizamiento interno es exactamente lo que compensa la diferencia de circunferencias. Por eso, aunque geométricamente cada punto del círculo menor se corresponda con uno del mayor, físicamente no todos esos puntos contribuyen a contacto o recorrido efectivo. El suelo sólo recibe la rodadura del círculo grande; la rueda interna aporta giro, pero no tracción.
Un poco de matemáticas
La paradoja de Aristóteles se vuelve aún más interesante cuando se introduce la expresión matemática de la longitud de una circunferencia. Si una rueda gira sin deslizar, el recorrido lineal que realiza al completar una vuelta es exactamente igual a su circunferencia, es decir:
donde L es la longitud recorrida, r es el radio de la rueda y π es la constante que relaciona la circunferencia con el diámetro. Si tenemos dos ruedas concéntricas de radios diferentes, R para la exterior y r para la interior, entonces sus respectivas longitudes son:
Aquí está el problema: al rodar una vuelta, la rueda grande en contacto con el suelo recorre 2πR, pero la pequeña, al ir acoplada y suspendida, no tiene contacto real. Si alguien pretendiera que también rueda sin deslizar, su desplazamiento debería ser 2πr, que es menor. Pero como se ha demostrado, en el conjunto ambas ruedas recorren 2πR. Esto viola la condición de rodadura pura para la rueda pequeña. Por tanto, no puede haber rodamiento sin deslizamiento simultáneamente en ambas circunferencias.
¿Y si la rueda pequeña toca el suelo? una solución menos conocida, pero igualmente válida
Aunque la solución basada en el deslizamiento de la rueda interna es la más citada, no es la única. Hay otra forma igualmente válida de resolver la paradoja, que suele pasar desapercibida. ¿Qué ocurre si en lugar de apoyar la rueda exterior sobre el suelo, dejamos que sea la rueda interior —la más pequeña— la que ruede sin deslizar? Esta posibilidad, que algunos denominan “caso II”, ofrece una explicación simétrica pero con consecuencias distintas, y ha sido utilizada tanto en demostraciones prácticas como en vídeos divulgativos de gran claridad visual.
Si se apoya la rueda pequeña directamente sobre la superficie y se hace rodar el conjunto acoplado (es decir, ambas ruedas giran solidariamente alrededor del mismo eje), lo que se observa es que la rueda menor sí cumple la condición de rodamiento sin deslizamiento. En consecuencia, la distancia total recorrida por el sistema es igual a la circunferencia de la rueda interior, es decir:
donde r es el radio de la rueda pequeña. Sin embargo, la rueda grande, al girar solidariamente, completa también una vuelta, lo que implicaría que debería haber recorrido una distancia igual a su propia circunferencia, mayor que la de la pequeña. Y, sin embargo, ambas han recorrido lo mismo, como conjunto. Esta contradicción aparente se resuelve reconociendo que en este caso, la rueda grande es la que está resbalando. No rueda sin deslizar: gira, pero su perímetro no se corresponde con un desplazamiento lineal propio, ya que no está en contacto con el suelo.
Este razonamiento es plenamente simétrico al caso anterior. En el primer análisis, se asumía que la rueda exterior estaba en contacto con el suelo, por lo que era la rueda pequeña la que deslizaba. En este segundo caso, es la rueda menor la que rueda correctamente, y la rueda grande la que no cumple con la condición de rodadura pura. Lo más importante es entender que no se puede aplicar la misma fórmula de desplazamiento a ambas ruedas a la vez si solo una de ellas mantiene contacto real y sin deslizamiento con la superficie.
Un ejemplo cotidiano de este segundo caso es el de una botella acostada que rueda sobre su cuello, o el de algunas ruedas de tren, que tienen una brida o reborde interior. En estos casos, es el perímetro pequeño el que está en contacto y el que determina la distancia real recorrida. La rueda exterior, por tanto, puede rotar completamente sin que ello implique que haya “caminado” por su propia circunferencia.
En resumen, la paradoja se puede resolver desde ambos puntos de vista, siempre que se tenga claro cuál es la circunferencia que está actuando como base de contacto sin deslizamiento. La clave está en identificar correctamente cuál de las dos ruedas cumple las condiciones ideales de rodamiento. Al hacerlo, desaparece el conflicto y las fórmulas físicas recuperan su validez. No hay contradicción, sino un malentendido sobre qué parte del sistema está realmente impulsando el movimiento.
Sigue sin convencerme lo de la fricción y el deslizamiento: ¿qué hago?
Es una reacción comprensible. Muchas personas, al ver la paradoja representada en un dibujo limpio, con dos circunferencias perfectas y sin contacto físico real, sienten que la explicación basada en la fricción y el deslizamiento complica más que aclara. Si todo es ideal, si nada toca nada, ¿por qué introducir un fenómeno físico como el roce o el patinaje? ¿No basta con la geometría?
Y en efecto: sí basta, si se asume que el problema es puramente matemático. Desde ese enfoque, lo que desconcierta no es el comportamiento de los cuerpos materiales, sino una propiedad profunda de la geometría: que dos curvas pueden tener una correspondencia punto a punto perfecta y, sin embargo, longitudes diferentes. La paradoja, entonces, no se resuelve hablando de cómo ruedan o se deslizan las ruedas, sino reconociendo que nuestra intuición sobre el infinito puede fallar. Ese es el verdadero núcleo del enigma.
Ahora bien, si la rueda está hecha de madera y rueda sobre una mesa, como en los vídeos que circulan por redes, entonces el problema deja de ser abstracto. En ese caso, sí hay una rueda que toca el suelo y otra que no, y ahí la fricción entra en juego. Pero si lo que te interesa es el concepto puro, la paradoja lógica sin distracciones materiales, puedes prescindir de toda referencia al rozamiento. No hay trampa ni contradicción: hay una idea sutil sobre el infinito y la medida. Y si eso te convence más que el chirrido de una rueda mal apoyada, estás en buena compañía: también convenció a Bolzano, Galileo y Cantor.
Referencias
- Mecánica (atrib. a Aristóteles), problema 24 – Paradoja de las ruedas de Aristóteles.
- Galileo Galilei (1638). Discorsi e dimostrazioni matematiche, intorno a due nuove scienze – Análisis del rodamiento con polígonos y vacíos infinitesimales.
- Bernard Bolzano (1851). Paradojas del infinito – Discusión sobre la biyección entre puntos de circunferencias de distinto tamaño.
- Marin Mersenne (1623). Quaestiones celeberrimae in Genesim – Reflexiones sobre el problema de la rueda y el movimiento relativo.




