En 1935, cuando Einstein hablaba de “acciones fantasmales a distancia”, se refería con escepticismo a una de las ideas más extrañas y contraintuitivas de la mecánica cuántica: el entrelazamiento. Desde entonces, esta propiedad ha pasado de ser una rareza conceptual a convertirse en una piedra angular de las tecnologías cuánticas emergentes. Sin embargo, su estructura matemática profunda y su comportamiento en distintos tipos de espacio siguen siendo un misterio, especialmente cuando se trata de sistemas en más de dos dimensiones.
Ahora, un equipo de físicos teóricos ha logrado algo notable: demostrar que el entrelazamiento cuántico obedece reglas universales en todas las dimensiones del espacio-tiempo, desde las más simples hasta las más complejas. Publicado en Physical Review Letters, el trabajo combina ideas de física de partículas, teoría cuántica de campos y teoría de la información, para revelar un patrón común que hasta ahora había escapado incluso a los enfoques más sofisticados.
Estructuras profundas en el caos cuántico
En física clásica, dos partículas que se encuentran a grandes distancias no tienen por qué estar relacionadas. Pero en el mundo cuántico, la información puede compartirse entre partículas de forma instantánea, aunque estén separadas por kilómetros. Este fenómeno, conocido como entrelazamiento cuántico, no solo ha sido demostrado en laboratorio, sino que también es crucial para tecnologías como la computación cuántica o las redes de comunicación seguras.
Lo que todavía se desconocía con precisión era cómo se comporta este entrelazamiento en sistemas de más de una dimensión espacial, un problema complejo tanto matemática como físicamente. La mayor parte de los estudios anteriores se centraban en modelos simplificados de una sola dimensión espacial más el tiempo (1+1), porque resultan más manejables desde el punto de vista técnico. Pero los investigadores querían saber si había una estructura común que se mantuviera al ampliar la cantidad de dimensiones.
Una herramienta poderosa importada desde la física de partículas
Para abordar este reto, el equipo de Yuya Kusuki (Kyushu University), Hirosi Ooguri (Caltech y Universidad de Tokio) y Sridip Pal (Caltech) recurrió a una estrategia poco convencional en este campo: la teoría térmica efectiva, una herramienta que ha tenido aplicaciones importantes en física de partículas pero rara vez se había utilizado en el ámbito de la información cuántica.
Este marco permite describir el comportamiento de sistemas complejos utilizando unos pocos parámetros clave, en lugar de lidiar con todos los detalles microscópicos. Gracias a esta simplificación, los autores fueron capaces de estudiar cómo se comporta una medida fundamental del entrelazamiento llamada entropía de Rényi, en diferentes tipos de sistemas y dimensiones.
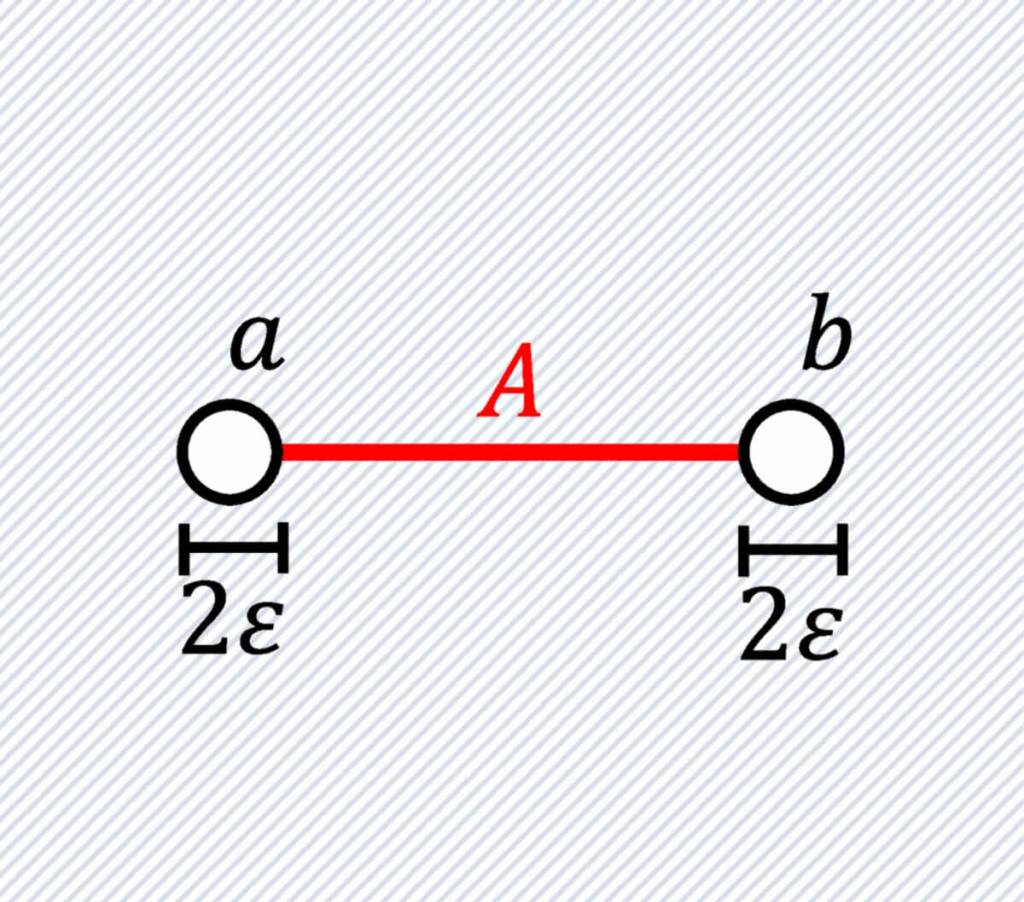
Una de las afirmaciones clave del artículo es que, en el límite cuando el número de réplicas tiende a cero, la entropía de Rényi para un dominio de entrelazamiento con frontera esférica se comporta de forma universal, siguiendo esta fórmula (solo para gente atrevida, te lo puedes saltar):
Aquí, f es una constante cosmológica que depende de la teoría, ϵ es un parámetro de corte ultravioleta y d es la dimensión del espacio-tiempo. Lo importante es que el comportamiento no depende de los detalles del sistema, sino solo de su dimensión y geometría, lo que implica una universalidad profunda.
Más allá del límite: espectros y fronteras
Además de confirmar este comportamiento universal en el límite n→0, los autores también exploraron cómo se distribuyen los valores propios del llamado Hamiltoniano modular, un operador que describe cómo está estructurada la información en el sistema cuántico. Este análisis permitió obtener una expresión aproximada para el espectro de entrelazamiento, algo esencial para comprender cómo se organiza la información en sistemas cuánticos extensos.
La investigación también abordó un aspecto técnico pero fundamental: las contribuciones de los bordes del dominio de entrelazamiento. En los cálculos, estas contribuciones aparecen como correcciones que decrecen con potencias de nn, pero que son importantes para entender cómo se aplica la fórmula en sistemas reales. En palabras del artículo: “La corrección subdominante de la frontera del dominio de entrelazamiento está suprimida por una potencia de n”.
Este detalle técnico no solo confirma la validez del método en distintos escenarios, sino que también abre el camino a futuros estudios sobre cómo se comportan los bordes en teorías conformes más generales.
¿Qué significa "número de réplicas" y por qué tiende a cero?
El número de réplicas, o replica number, es un parámetro matemático que aparece cuando se utiliza el método de réplicas para calcular cantidades como la entropía de Rényi o la entropía de entrelazamiento en sistemas cuánticos.
En lugar de calcular directamente la entropía de un sistema —algo muy difícil cuando se trata de muchos estados entrelazados—, se considera una especie de “truco” matemático: copiar el sistema n veces (las “réplicas”), calcular una cierta cantidad en ese sistema replicado, y luego extrapolar el resultado al valor que realmente se busca.
El límite n→0 puede parecer extraño al principio, pero es común en este tipo de técnicas. En este contexto, se estudia el comportamiento del sistema cuando el número de copias tiende a cero, porque eso permite acceder a ciertas propiedades del espectro de entrelazamiento y entender cómo se comporta la información cuántica en estados muy complejos.

El límite de las ideas brillantes: la "zona caliente"
En física cuántica, a veces los métodos brillantes tienen sus propias limitaciones. Uno de los enfoques mencionados en el trabajo es la "hot spot idea", que sugiere que en ciertos límites, como cuando la temperatura efectiva diverge en ciertas regiones, los resultados se ven dominados por contribuciones locales. Este método había sido útil en dos dimensiones para derivar fórmulas exactas. Pero los autores muestran que en dimensiones superiores, la divergencia del gradiente térmico hace que el método pierda validez.
Como explican en el paper: “Los términos de orden superior contribuyen al mismo orden que el término cosmológico, y la expansión en temperatura alta falla cerca de la zona caliente”.
Esto no invalida la aproximación global, pero indica claramente dónde dejan de aplicarse ciertas intuiciones válidas en teorías más simples.
Aplicaciones futuras: desde simulaciones hasta gravedad cuántica
Aunque el trabajo es fundamentalmente teórico, sus implicaciones son notables. En primer lugar, puede contribuir a mejorar los métodos numéricos de simulación para sistemas cuánticos de muchas partículas. También puede ofrecer nuevas claves para clasificar estados cuánticos complejos, algo crucial para avanzar en la computación cuántica.
Pero lo más ambicioso es que este marco podría aportar una nueva perspectiva para abordar problemas en física de fronteras, como la paradoja de la pérdida de información en agujeros negros o la estructura de la gravedad cuántica. En sistemas holográficos, donde las teorías cuánticas tienen equivalentes gravitacionales, estas fórmulas universales pueden usarse como pruebas de consistencia, o incluso como herramientas para descubrir nuevas dualidades.
Referencias
- Yuya Kusuki, Hirosi Ooguri, Sridip Pal. Universality of Rényi Entropy in Conformal Field Theory. Physical Review Letters (2025). DOI: 10.1103/fsg7-bs7q.




