Cuando una persona estornuda, el aire que expulsa no se desplaza en línea recta ni de forma ordenada. ¡Parece contradecir las leyes de Newton! Se enrosca, se disgrega, se arremolina. Lo mismo ocurre con el humo que sale de una chimenea, con las corrientes marinas o con una tormenta en desarrollo. Todos estos fenómenos tienen algo en común: son ejemplos de turbulencia, un tipo de flujo caótico que ha desconcertado a físicos, ingenieros y matemáticos durante más de un siglo.
En 1964, Richard Feynman definió la turbulencia como "el problema no resuelto más importante de la física clásica". Y no le faltaba razón. Pese a su omnipresencia en la naturaleza y en la vida cotidiana, la turbulencia es extremadamente difícil de describir y predecir con precisión. Ahora, un nuevo modelo matemático desarrollado por Björn Birnir (Universidad de California, Santa Barbara) y Luiza Angheluta (Universidad de Oslo) aporta una clave fundamental para comprender cómo evoluciona este fenómeno en una de sus formas más esquivas: la turbulencia lagrangiana.
Por qué la turbulencia lagrangiana es un reto aún mayor
No todas las turbulencias son iguales. La forma más habitual de estudiarlas es a través del llamado enfoque euleriano, en el que se observa el flujo desde un punto fijo. Pero la turbulencia lagrangiana funciona distinto: consiste en seguir a las partículas individuales dentro del fluido, como si fuéramos montados en ellas.
Este enfoque introduce un nivel de complejidad mayor porque implica no solo registrar posiciones, sino también analizar las trayectorias y los cambios de velocidad de cada partícula a lo largo del tiempo. A pesar de los avances tecnológicos en simulaciones por ordenador, entender con precisión cómo se comportan estas partículas ha sido un enorme desafío.
Birnir y Angheluta abordaron este problema mediante una teoría estadística conocida como Stochastic Closure Theory, que permite incorporar el azar inherente a los sistemas turbulentos. El modelo resultante, según los autores, identifica con claridad tres etapas diferenciadas en la evolución de un flujo turbulento: una inicial de tipo balístico, otra intermedia lagrangiana, y una final euleriana.
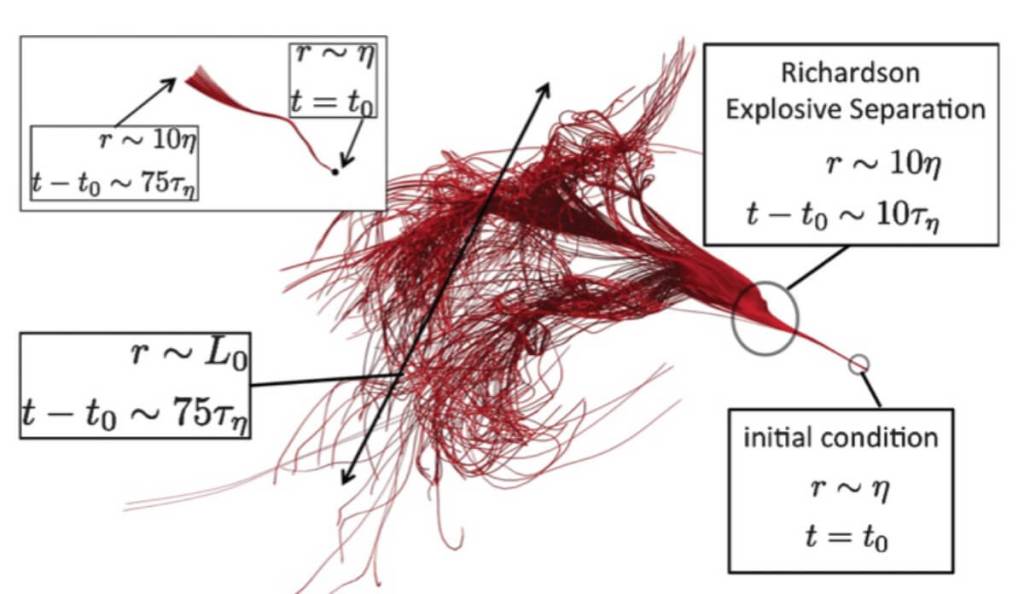
Tres fases, tres escalas
El trabajo define con precisión cómo cambian las propiedades estadísticas del flujo a lo largo del tiempo. La primera etapa, llamada balística, se da cuando todas las partículas se mueven casi juntas, con una separación que crece de forma lineal con el tiempo. Es un régimen de movimiento predecible, aunque breve.
A continuación, aparece el comportamiento lagrangiano. Aquí, las partículas comienzan a separarse de forma acelerada, siguiendo patrones más caóticos pero con una estructura estadística definida. Según el paper, “las funciones de estructura presentan un régimen de escalado lagrangiano sin intermitencia, y luego pasan a un régimen euleriano con intermitencia”. Es decir, las fluctuaciones en la velocidad entre partículas se vuelven más erráticas conforme el sistema entra en la fase final.
La tercera etapa, la euleriana, corresponde a un estado donde la turbulencia parece más homogénea y contiene vórtices más pequeños y complejos. Cada fase tiene su propio conjunto de leyes matemáticas que permiten describir cómo varía la velocidad entre partículas separadas por una cierta distancia y durante un tiempo determinado.

Una transición que por fin se puede describir
Hasta ahora, la región intermedia entre los regímenes balístico y euleriano era poco comprendida. Muchos investigadores habían notado su existencia, pero no contaban con una teoría matemática que la explicara con precisión. Lo que Birnir y Angheluta han hecho es ofrecer un modelo que no solo identifica esta “región de paso” (passover region), sino que también detalla su dinámica.
Utilizando relaciones generalizadas de Green-Kubo-Obukhov, los autores demuestran cómo esta transición puede ser descrita en términos de las funciones de estructura del flujo. En palabras del estudio, “el tiempo de transición para la región de paso está controlado por la segunda función de estructura”, lo que permite conectar las tres etapas mencionadas dentro de un mismo marco teórico.
Este avance es crucial porque permite entender cómo se comporta un flujo turbulento a distintas escalas de tiempo y espacio. Es especialmente relevante para fenómenos donde una pequeña diferencia inicial puede llevar a grandes divergencias posteriores, como ocurre con la dispersión de partículas contaminantes o patógenos.

Aplicaciones en salud, clima y tecnología
La utilidad del nuevo modelo no se limita a la teoría. Sus implicaciones prácticas abarcan desde la predicción de huracanes hasta el control de enfermedades respiratorias. El propio Birnir ha destacado su interés en aplicar esta herramienta a estudios biomédicos: “Esto nos da una base más sólida para calcular cosas como la propagación del COVID y otros aerosoles”.
Además, el modelo también se puede aplicar para simular con más realismo cómo se mezclan los fluidos en procesos industriales, cómo se diseminan las partículas en nubes o cómo evolucionan las corrientes oceánicas. Todos estos sistemas comparten una característica esencial: presentan turbulencias que cambian con el tiempo y requieren modelos dinámicos para ser comprendidos.
Un aspecto especialmente innovador del estudio es la identificación de una cuarta etapa en la evolución de la turbulencia: los “remolinos libres” o free eddies. Se trata de vórtices que se separan del flujo principal y mantienen su energía durante un tiempo prolongado, lo que puede ser clave para entender los procesos de decaimiento de la turbulencia.
Más cerca de una teoría unificadora
La turbulencia es, en esencia, un fenómeno multiescala. Involucra procesos que ocurren simultáneamente en fracciones de segundo y en escalas de kilómetros. Por eso, uno de los mayores retos ha sido siempre encontrar una teoría que funcione en todos los niveles, desde el movimiento inicial de una partícula hasta la dinámica global del sistema.
El modelo de Birnir y Angheluta logra conectar de forma coherente diferentes escalas temporales y espaciales mediante funciones matemáticas que se ajustan a los datos experimentales. En las simulaciones que acompañan el estudio, puede verse cómo las predicciones del modelo coinciden de forma notable con los resultados obtenidos a partir de datos reales.
Además, los autores han probado que el uso del tiempo como variable de referencia (en lugar de otras como la separación entre partículas) permite eliminar distorsiones en los análisis, lo cual representa una mejora significativa en la interpretación de los datos. Como se afirma en el artículo: “Parece mejor tomar la derivada logarítmica con respecto al tiempo t, en lugar de con respecto a S₂, para entender completamente los distintos regímenes de escalado”.
Referencias
- Björn Birnir y Luiza Angheluta, Scaling of Lagrangian structure functions, Physical Review Research, 2025. DOI: 10.1103/PhysRevResearch.7.023225.




