Este artículo busca acercar al lector algunas de las ideas contenidas en un estudio galardonado con el premio a la “Mejor contribución metodológica en el campo de la Estadística”, otorgado por la Sociedad de Estadística e Investigación Operativa y la Fundación BBVA [1].
1. Estadística con curvas
Tradicionalmente, los resultados de los experimentos científicos se limitaban a valores numéricos concretos, como la velocidad de caída de un objeto o la temperatura corporal de una persona. Hoy en día, los avances tecnológicos permiten registrar de forma (casi) continua esos datos, convirtiéndolos en curvas: en lugar de medir la velocidad de llegada al suelo del objeto, se dispone de su velocidad (casi) instantánea durante toda la caída, o de la evolución de la temperatura de una persona a lo largo de todo un día. Este hecho ha requerido la creación de técnicas estadísticas específicas para el manejo de curvas, dando lugar al Análisis de Datos Funcionales (FDA por su nombre inglés) [2, 3].
En ciencia, es habitual construir modelos matemáticos que simplifican, en cierta medida, la realidad. El modelo de regresión lineal, cuyo origen se remonta al siglo XIX, es uno de los pilares de la estadística moderna. Este modelo plantea la relación Y = β0 + β1 X + ε entre dos variables numéricas X e Y que incluye un error aleatorio ε. Sin embargo, es obvio que para adoptar un modelo matemático hay que comprobar su ajuste al fenómeno que pretende modelar. La posible sobresimplificación impuesta por un modelo puede no ajustarse a la realidad, creando vacas esféricas o prediciendo que una niña se jubilará midiendo más de cuatro metros si utilizamos una regresión lineal que se ajusta bastante bien sus alturas desde los tres a los trece años.
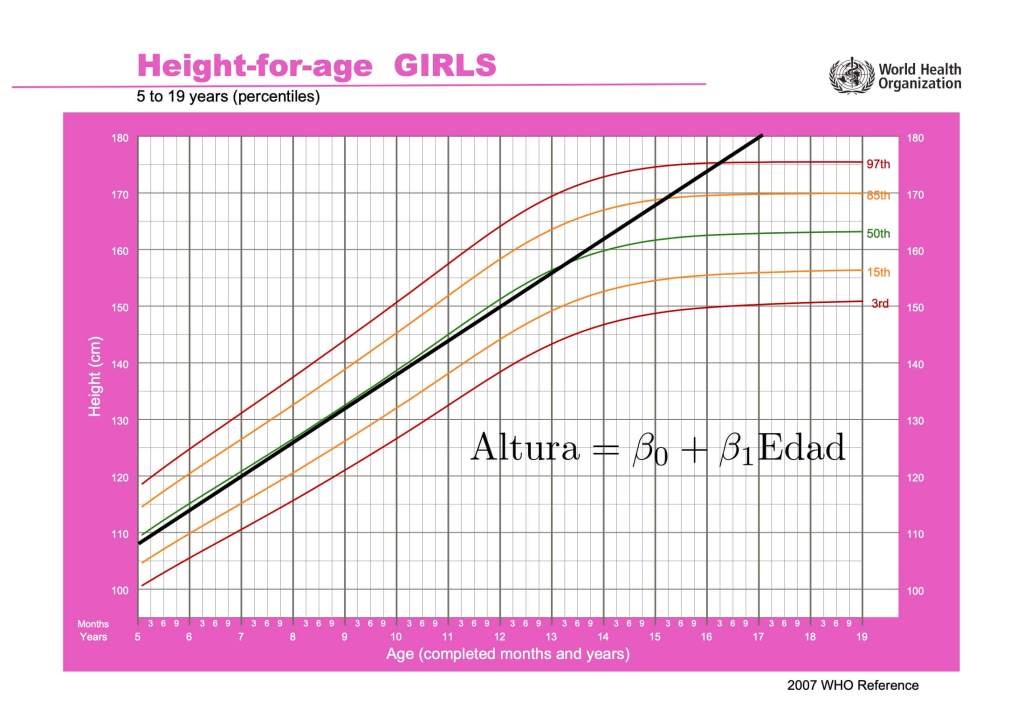
El objetivo de [1] es evaluar el ajuste de un modelo de regresión lineal cuando se pretende utilizar una curva para predecir una variable numérica, concluyendo mediante un test de validez si en los datos existen discrepancias significativas con la predicción del modelo. El interés del contraste de hipótesis radica en que, cuando trabajamos con curvas, no disponemos de intuición gráfica para valorar si la regresión lineal puede ser razonable o no.
El modelo de regresión lineal destaca tanto por su simplicidad como por la variedad de situaciones en las que es aplicable. Un ejemplo de su empleo es usar la curva del número de infectados con cierto virus hasta hoy para predecir cuántos nuevos infectados van a surgir durante la semana que viene. Otro ejemplo es determinar el contenido de grasa de una pieza de carne a partir de una curva que describe cómo absorbe radiaciones de distintas longitudes de onda.
El contraste de hipótesis propuesto en [1] para evaluar el modelo de regresión lineal utiliza la simplificación proporcionada por las proyecciones aleatorias. Esta herramienta “comprime” cada curva en un número “representativo” de la misma. Esto simplifica notablemente el contraste del modelo, ya que, en vez de una curva y una variable numérica, se trabaja con dos variables numéricas. Un aspecto clave para esta “representatividad” es el carácter aleatorio de las proyecciones.
2. ¿Qué es una proyección?
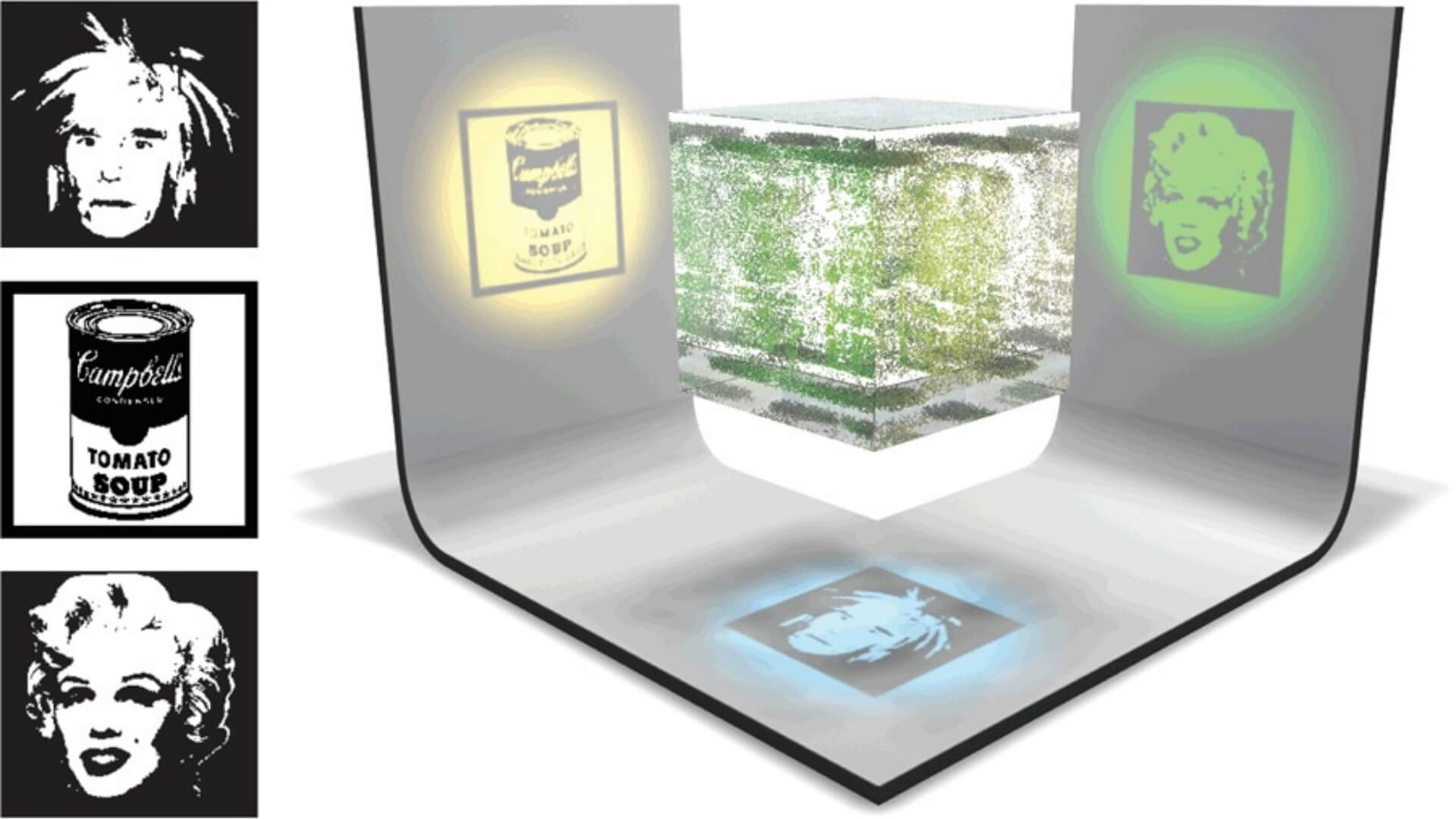
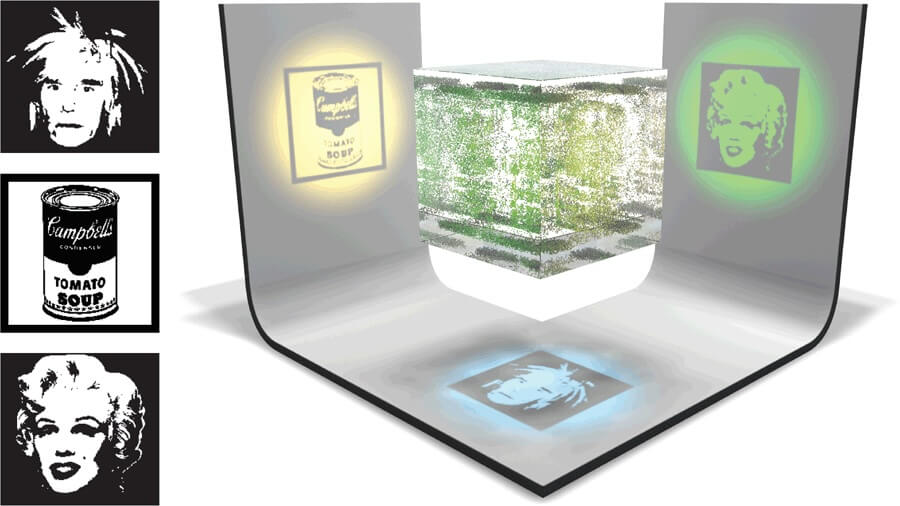
La palabra proyección en matemáticas es (casi) equivalente a sombra. Si suspendemos en el aire una pelota y la iluminamos desde arriba con una linterna, la sombra que aparece en el suelo es su proyección sobre él.
Podemos identificar la linterna con un punto que emite rayos de luz en cierto embudo de direcciones. En Estadística, en lugar de linternas, se suelen usar “pantallas de rayos X” o pantallas luminosas, que son superficies planas formadas por infinitos puntos que emiten rayos perpendiculares a dicha superficie. Si iluminamos la pelota con una de ellas situada en el techo, la sombra proyectada es una circunferencia con radio igual al de la pelota. Si tomamos otra pelota de diferente tamaño, la sombra será también circular, pero las distinguiremos por el tamaño de sus radios. Pero si cogemos un balón de rugby, sucede que la sombra solo es una circunferencia si el eje más largo del balón es perpendicular a la pantalla. Obtendremos una elipse si es paralelo y sombras asimétricas en las demás orientaciones.

Los rayos X atraviesan un objeto perdiendo parte de su energía, absorbida por dicho objeto. Esta absorción depende de la composición y espesor del objeto que atraviesan: si el rayo X llega a una pantalla blanca sin interferencias, su energía quema el punto de llegada y este se vuelve negro. En caso de que el objeto absorba completamente el rayo, el punto de llegada no recibe energía y permanece blanco. Los tonos grises indican una absorción parcial de la energía del rayo por parte del objeto.
Con esta analogía, a diferencia de los rayos luminosos, los rayos X permiten, por ejemplo, distinguir un huevo de madera de otro de gallina con, exactamente, la misma forma y tamaño. El de madera tendrá una sombra más o menos homogénea (aunque más oscura en los bordes, porque se atraviesa menos madera), mientras que la sombra del de gallina mostrará con claridad la yema que hay en su interior, porque la yema y la clara absorben de manera diferente los rayos X.
Por lo tanto, si tenemos dos objetos diferentes (por forma o composición) y diseñamos un emisor del estilo de los de rayos X, en el que los rayos sean parcialmente absorbidos, las proyecciones de ambos objetos van a permitir saber cuál es cuál, a no ser que los objetos que se van a proyectar tengan cierta similitud y, además, los coloquemos muy cuidadosamente. En otras palabras: si elegimos al azar la posición de un balón de rugby, con total seguridad su proyección va a delatar que no es esférico.1 El posicionamiento al azar es clave para evitar engaños de objetos cuidadosamente construidos para proyectar sombras que no son representativas de su estructura (ver [4] para una colección de ejemplos inspiradores).
3. Proyecciones en Estadística
A partir de ahora, balones y huevos van a ser reemplazados por nubes de puntos en dimensión dos, tres o superior. Estos conjuntos de datos están formados por 𝑛 vectores Xi = (Xi1,…,Xip ), 𝑖 = 1,…,𝑛, de dimensión 𝑝 que aparecen cuando se miden simultáneamente 𝑝 variables numéricas. Ejemplos de datos tridimensionales (𝑝 = 3) son el peso, la altura y la presión sanguínea de personas. Pero la tecnología permite medir muchas variables al mismo tiempo y no es raro encontrar situaciones con millares de dimensiones, lo que aumenta la complejidad de los objetos considerablemente. Para distinguir estos objetos necesitaremos un emisor-receptor de rayos X adecuado.
Haremos dos suposiciones importantes:
- 3.1 Para cada conjunto de datos hay un patrón (llamémosle patrón poblacional) que determina cómo se distribuyen estos datos.
- 3.2 Los datos que tenemos son una muestra obtenida de cierta población, y, por lo tanto, siguen el patrón poblacional que corresponda.
Las pantallas planas emisoras de rayos X tienen sentido en dimensión tres. En dimensión cuatro aparece un problema (que se mantiene en dimensiones superiores): habría que usar pantallas tridimensionales. Pero, ¿qué es una pantalla tridimensional? ¿Cómo vemos las absorciones? El uso de pantallas de dimensión superior a dos no parece ni sencillo ni de utilidad.
La búsqueda de un buen emisor-receptor de rayos X, que sea manejable en cualquier dimensión, se resuelve de modo sorprendentemente sencillo: ¿y si usamos un alambre como receptor en todas las dimensiones? En dimensión tres solo hay que usar una pantalla emisora cilíndrica lo suficientemente grande como para contener la nube proyectada y situar un alambre en el eje del cilindro. Podemos imaginar que todos los puntos de la superficie interior de la pantalla emisora cilíndrica emiten rayos con la misma energía hacia el eje central. Si nos fijamos en el punto situado a altura x del eje del cilindro, como las absorciones solo se producen por choques con puntos de la nube, midiendo la energía de cada rayo a la llegada, sabemos cuántos choques ha sufrido y, como no puede haber un punto que interfiera con dos rayos, sumando el número de choques sabemos el número de puntos de la nube que están situados a la altura x.
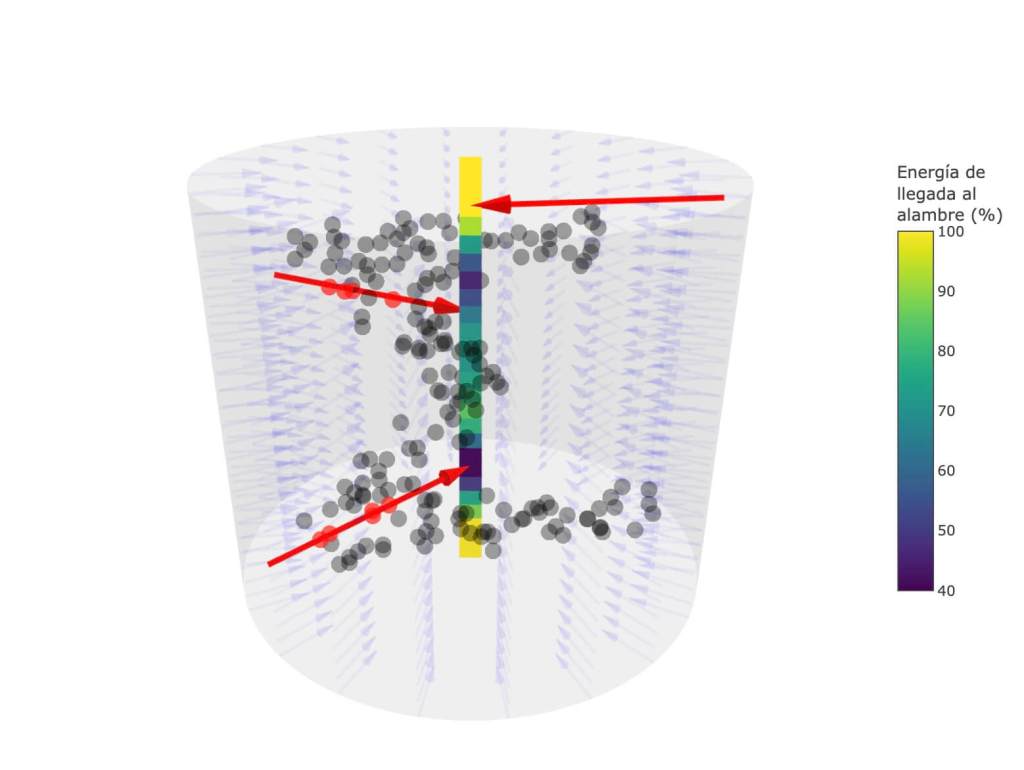
En consecuencia, podemos olvidarnos de los rayos X, del cilindro y de todo, menos del alambre central. Vamos a fijar la recta que representa a este alambre. Lo único que tenemos que hacer es coger el punto que está a altura x en esta recta y mirar cuántos puntos de la nube están a esta misma altura.
Matemáticamente, esta operación está relacionada con el producto escalar de dos vectores, Xi (dato) y h = (h1,…,hp ) (colineal con el eje del cilindro), que se define como el número
Esta operación permite comprimir el conjunto de datos 𝑝-dimensional {X1,…,Xn } al conjunto de datos proyectado {X1 ⋅ h,…,Xn ⋅ h }, ahora contenido en dimensión uno. En el caso del cilindro de la figura 4, tomamos h = (0,0,1) y el producto escalar nos proporciona las terceras coordenadas de la nube de puntos tridimensional. Es obvio que esta construcción puede hacerse en cualquier dimensión, no solo en 𝑝 = 3.
Ahora bien, ¿mantiene esta compresión la información de los datos? La respuesta es afirmativa con matices. Si elegimos la recta h al azar, el resultado principal de [5] muestra que, si hacemos las proyecciones con dos nubes de puntos con patrones diferentes, ¡es imposible que los patrones de las proyecciones coincidan! Por lo tanto, podemos distinguir patrones en los datos originales a partir de sus proyecciones aleatorias.
4. Proyecciones aleatorias en la práctica
En el punto 3.2 hemos dicho que suponemos que se eligen muestras usando determinado patrón poblacional. Pero es bien conocido que las muestras tienen cierta variabilidad natural. Por ello, aun teniendo dos patrones idénticos de partida, esta variabilidad va a hacer imposible que dos muestras obtenidas con el mismo patrón coincidan exactamente.
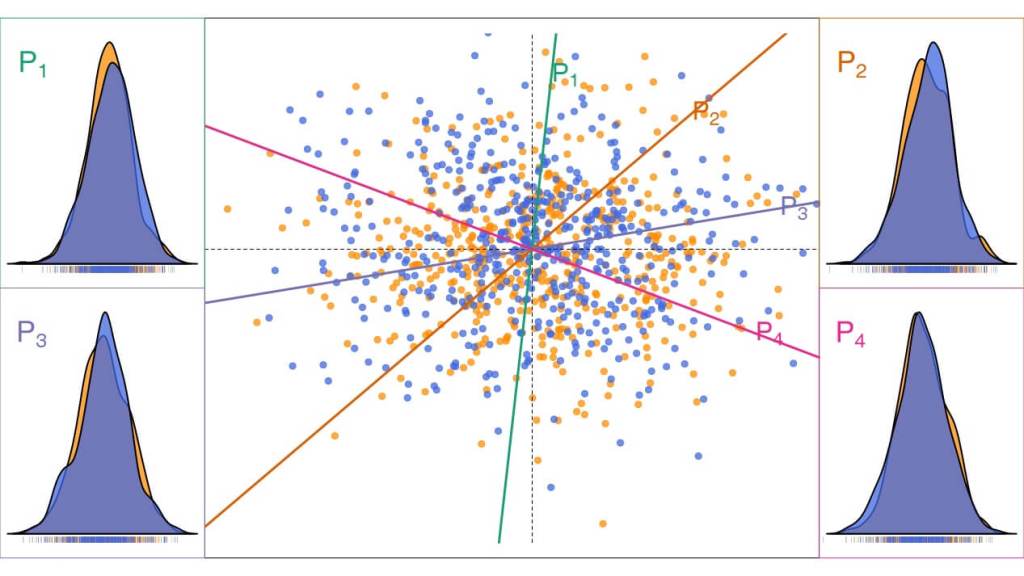
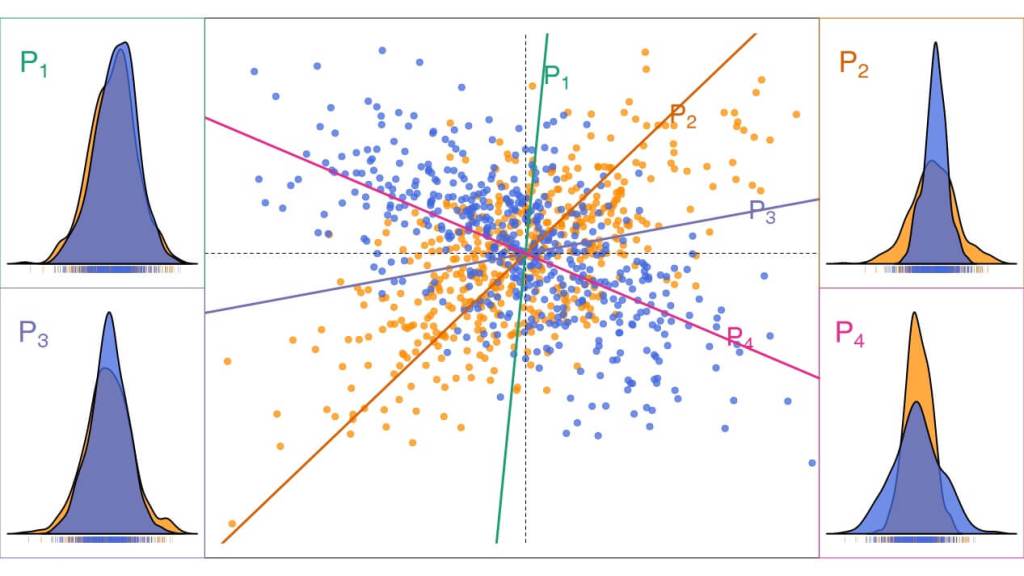
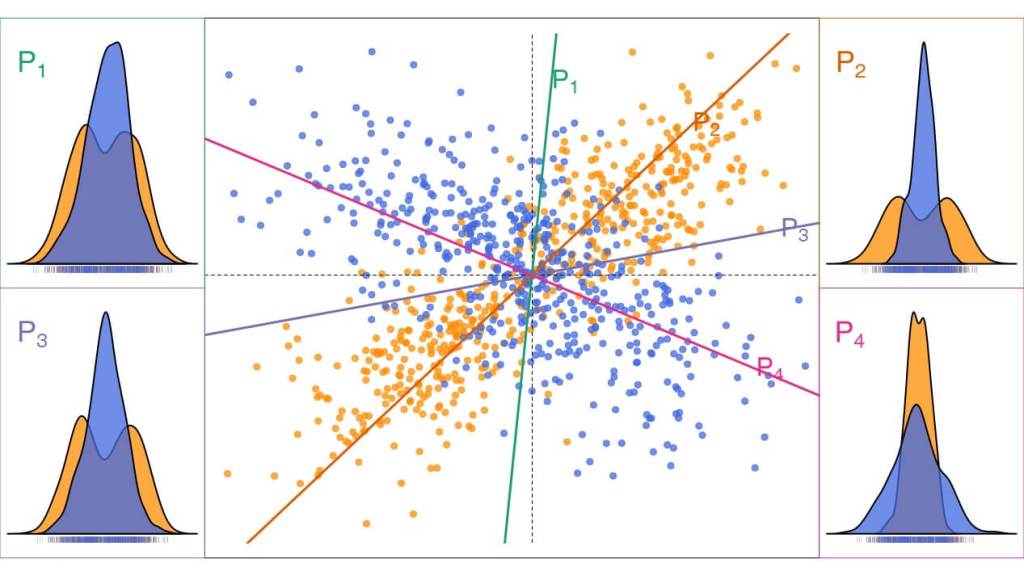
Cada una de las figuras 5, 6 y 7 contiene dos muestras de 500 puntos tomadas de dos poblaciones. Las poblaciones son idénticas en la figura 5, diferentes pero parecidas en la 6 y muy diferentes en la 7. Además, se han calculado cuatro proyecciones sobre los ejes señalados que han sido elegidos aleatoriamente. En las esquinas de las cuatro figuras, se muestran cuatro gráficos que, en el pie, recogen las proyecciones obtenidas (cada rayita vertical corresponde a la proyección de un punto) y, encima, una estimación de la densidad de probabilidad (patrón) que las produjo.
En la figura 5 estas gráficas deberían haber sido idénticas, pero la variabilidad de las muestras hace que aparezcan pequeñas diferencias entre ellas. Las muestras de la figura 6 tienen proyecciones claramente diferentes, excepto que se elija como recta el eje vertical o el horizontal.2 Como la recta P1 está próxima al eje vertical, resulta que las diferencias entre las dos proyecciones en esta recta son pequeñas. Pero a medida que nos alejamos de esta recta, las diferencias entre las proyecciones aumentan. Finalmente, las dos poblaciones involucradas en la figura 7 son tan diferentes, que sus proyecciones no se parecen en ninguna de las rectas elegidas.
Estos hechos plantean dos problemas:
- 4.1 ¿Qué diferencia tiene que haber entre las proyecciones para que estemos razonablemente seguros de que no se deben al azar? Una vez resuelta esta cuestión, tendríamos un procedimiento para poder afirmar con seguridad que dos nubes proceden de patrones diferentes.
- 4.2 Aunque según la teoría de [5], con suficientes datos, una única proyección es suficiente para distinguir entre dos patrones diferentes, la figura 5 muestra que, en la práctica, el azar puede elegir una dirección en la que las diferencias entre proyecciones sean similares a las esperadas por el azar.
Está claro que, si se soluciona el primer punto y se dispone de una herramienta de proyección, podemos analizar la semejanza o diferencia entre patrones de objetos complejos (curvas o datos de alta dimensión) simplemente analizando diferencias entre sus valores proyectados (números), que es una tarea más asequible.
5. De vuelta a las curvas
Los problemas 4.1 y 4.2 han sido resueltos en [1] para construir el test de validez del modelo de regresión lineal cuando la variable X (t ) es una curva (por ejemplo, dependiente del tiempo t ). Este modelo establece que existe una función β (t ) desconocida, de modo que cada curva X (t ) tiene asociado un valor numérico de Y determinado por
donde ε es un error aleatorio. La proyección de la curva X (t ) en la dirección determinada por la curva h (t ) se define como
lo que representa una extensión natural del producto escalar entre dos vectores.
La solución del problema 4.1 ocupa la mayor parte de [1] porque es técnica y compleja. La complejidad proviene de que la dimensión del espacio de curvas es infinita, lo que dificulta la estimación de β (t ).
La solución del problema 4.2 es más sencilla. Consiste en elegir varias direcciones de proyección y usar los resultados para decidir.3 La experiencia muestra que la posibilidad de distinguir entre patrones diferentes aumenta bastante utilizando entre 5 y 15 proyecciones aleatorias.
En conclusión, las proyecciones aleatorias son una herramienta de uso sencillo, que permite responder al complejo problema de decidir si la relación entre una población de curvas y una de respuestas numéricas puede ser lineal. El lector interesado en profundizar en las contribuciones técnicas del trabajo puede encontrar en [6] una exposición más detallada.
Notas
- El balón de rugby se delata siempre que su eje mayor no coincida exactamente con la perpendicular de la pared roja.
- Estos ejes se comportan igual que el eje mayor del balón de rugby.
- Una solución puede ser aplicar el test a las proyecciones disponibles y quedarse con la dirección en que los patrones son más diferentes; pero también se pueden promediar los resultados del test en todas las direcciones.
Referencias
- [1] Cuesta-Albertos, J.A., García-Portugués, E., Febrero-Bande, M. y González-Manteiga, W. (2019). Goodness-of-fit tests for the functional linear model based on randomly projected empirical processes. The Annals of Statistics, 47(1), 439–467. doi:10.1214/18-AOS1693.
- [2] Cuevas, A. (2014). A partial overview of the theory of statistics with functional data. Journal of Statistical Planning and Inference, 147, 1–23. doi:10.1016/j.jspi.2013.04.002.
- [3] Wang, J.-L., Chiou, J.-M., Müller y H.-G. (2016). Functional data analysis. Annual Review of Statistics and Its Application, 3, 257–295. doi:10.1146/annurev-statistics-041715-033624.
- [4] Mitra, N. J. y Pauly, M. (2009). Shadow art. ACM Transactions on Graphics, 28(5):1–7. doi:10.1145/1618452.1618502. En acceso abierto a través de https://graphics.stanford.edu/~niloy/research/shadowArt/shadowArt_sigA_09.html.
- [5] Cuesta-Albertos, J.A., Fraiman, R. y Ransford, T. (2007). A sharp form of the Cramer–Wold theorem. Journal of Theoretical Probability, 20, 201–209. doi:10.1007/s10959-007-0060-7.
- [6] Cuesta-Albertos, J.A., García-Portugués, E., Febrero-Bande, M. y González-Manteiga, W. (2024). Tests de bondad de ajuste para el modelo lineal funcional basados en proyecciones. Boletín de Estadística e Investigación Operativa, 40(3), 7–20. https://www.seio.es/wp-content/uploads/2024_40_3_BEIO_Estadistica.pdf
Juan Antonio Cuesta Albertos
Doctor en Ciencias Matemáticas

Eduardo García Portugués
Doctor en Estadística e Investigación Operativa

Manuel Febrero Bande
Doctor en Estadística e Investigación Operativa

Wenceslao González Manteiga
Doctor en Estadística e Investigación Operativa