Una pizarra cubierta de ecuaciones, un telescopio en la azotea de una colina italiana, dos sacerdotes con formación científica... y una pregunta que ha intrigado a generaciones de físicos: ¿podría existir más de una manera válida de describir el universo? El Observatorio Vaticano, más conocido por sus estudios astronómicos, ha sido el escenario de una investigación que podría abrir nuevas puertas a la comprensión de la gravedad, los agujeros negros y el origen del cosmos.
Los protagonistas son dos científicos del Vaticano, Gabriele Gionti y Matteo Galaverni, ambos sacerdotes católicos, que han publicado un trabajo en la revista European Physical Journal C con implicaciones profundas. Utilizando herramientas matemáticas avanzadas, han demostrado que existen dos formas distintas de representar la gravedad —el “marco de Jordan” y el “marco de Einstein”— que pueden ser equivalentes bajo ciertas condiciones, pero que, si esa equivalencia se rompe, pueden describir universos diferentes. Una afirmación tan audaz como rigurosa.
Dos formas de ver la gravedad
En el corazón del estudio se encuentra una pregunta técnica, pero de gran trascendencia: ¿cómo describir la gravedad cuando se añade un campo escalar, es decir, un tipo de energía adicional? Esta situación no es meramente teórica. Muchos modelos actuales que intentan unificar la relatividad con la física cuántica, o explicar la materia oscura, incluyen este tipo de campos.
Para abordarlo, los investigadores compararon dos “lenguajes” matemáticos distintos: el marco de Jordan y el marco de Einstein. Ambos parten de una misma teoría, pero reorganizan las ecuaciones y sus variables de formas diferentes. Lo sorprendente, como muestra el artículo, es que ambas descripciones son válidas, siempre que se cumplan ciertas condiciones bien definidas.
La herramienta clave para demostrar esta equivalencia fue el formalismo ADM-Hamiltoniano, una técnica matemática utilizada para analizar sistemas dinámicos complejos. Aplicando este enfoque, los autores mostraron que los dos marcos, aunque formulados de forma distinta, describen la misma física si se fijan correctamente los parámetros.
Las condiciones ocultas del universo
Pero esta equivalencia no es automática. En palabras del artículo, "la correspondencia permanece oculta" si no se imponen ciertas condiciones técnicas. Es decir, los dos marcos matemáticos solo son intercambiables si se sigue un procedimiento preciso y se consideran elementos que, en estudios anteriores, habían sido ignorados.
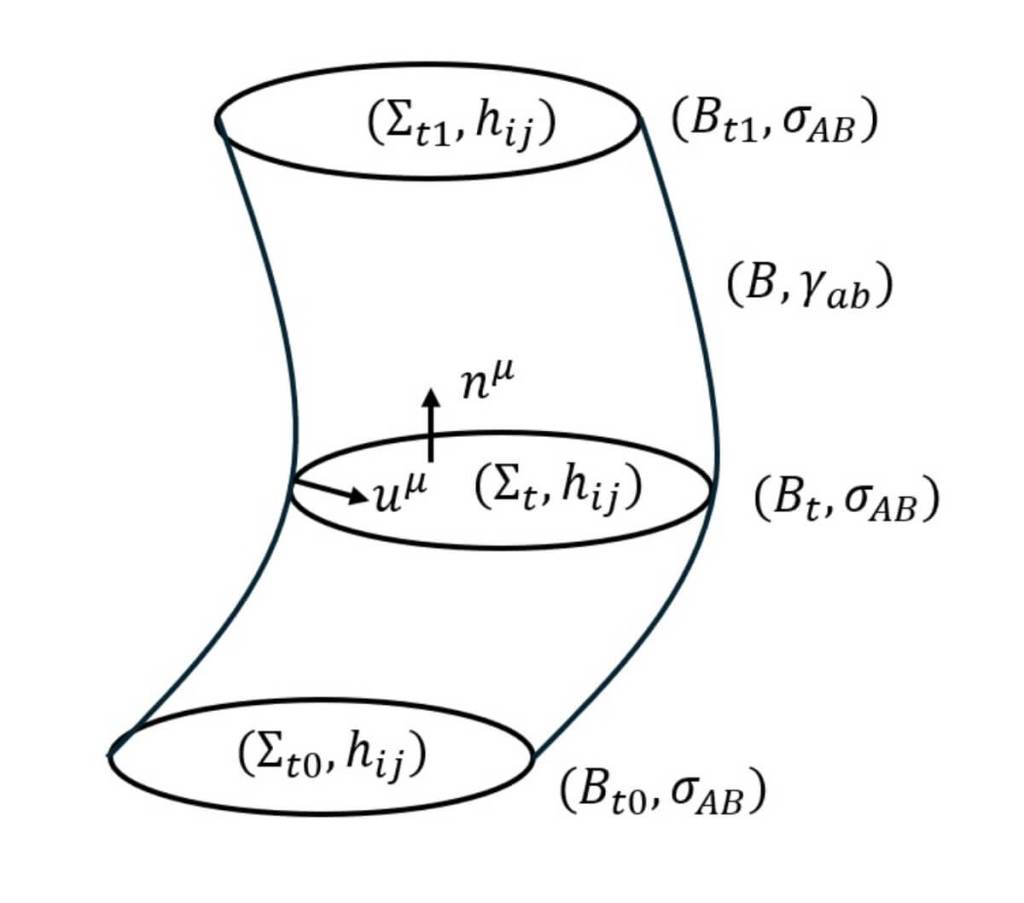
Uno de los elementos más cruciales —y descuidados hasta ahora— son los llamados términos de borde. Estos aparecen en los límites del espacio-tiempo que se estudia y, aunque suelen descartarse en muchos tratamientos simplificados, resultan esenciales para obtener las ecuaciones de movimiento completas. Como afirman los autores, “hay que considerar bien los términos de borde. Es la única manera de obtener las ecuaciones de movimiento correctas”.
Este paso puede parecer técnico, pero es fundamental. Ignorar estos términos daba lugar a ecuaciones parciales, incapaces de describir correctamente fenómenos complejos como los agujeros negros o las singularidades. Gracias a esta corrección, ahora es posible obtener soluciones exactas y consistentes en ambos marcos.
Cómo una fórmula puede cambiarlo todo: explicando el corazón matemático del hallazgo
Uno de los pilares del artículo de Gionti y Galaverni es el uso del formalismo ADM-Hamiltoniano, una herramienta matemática que permite reformular las ecuaciones de la relatividad general en términos de energía y evolución temporal. Esto resulta especialmente útil cuando se quiere estudiar la equivalencia entre distintos marcos, como el marco de Jordan y el marco de Einstein, en teorías que incluyen campos escalares.
El paso clave para demostrar esa equivalencia consiste en escribir el llamado Hamiltoniano, una función que describe toda la dinámica del sistema físico. En este contexto, el Hamiltoniano se construye a partir del lagrangiano, añadiendo los términos correspondientes a las fronteras del espacio-tiempo, conocidos como términos de borde. Su inclusión marca una diferencia sustancial.
Una forma simplificada del Hamiltoniano total (sin los detalles técnicos del tensor métrico y sus derivadas) es la siguiente:
H = ∫(N𝓗 + Nⁱ𝓗ᵢ) d³x + B
Donde:
- H es el Hamiltoniano total del sistema.
- N es la función de lapse (tiempo entre hipersuperficies).
- 𝓗 es la Hamiltoniana escalar, que recoge la densidad de energía.
- Nⁱ son las funciones de shift, relacionadas con el movimiento en el espacio.
- 𝓗ᵢ es la Hamiltoniana vectorial, relacionada con los momentos lineales del sistema.
- B representa los términos de borde, es decir, los efectos en las fronteras del espacio considerado.
¿Por qué es tan importante el término B? Porque sin él, la variación del Hamiltoniano no produce las ecuaciones de movimiento correctas. Esto significa que trabajos anteriores que omitían esos términos podían dar lugar a soluciones erróneas o incompletas. Al introducir correctamente B, los autores logran derivar ecuaciones completas en ambos marcos, algo imprescindible para evaluar su equivalencia o diferencia real.
Singularidades y nuevos universos
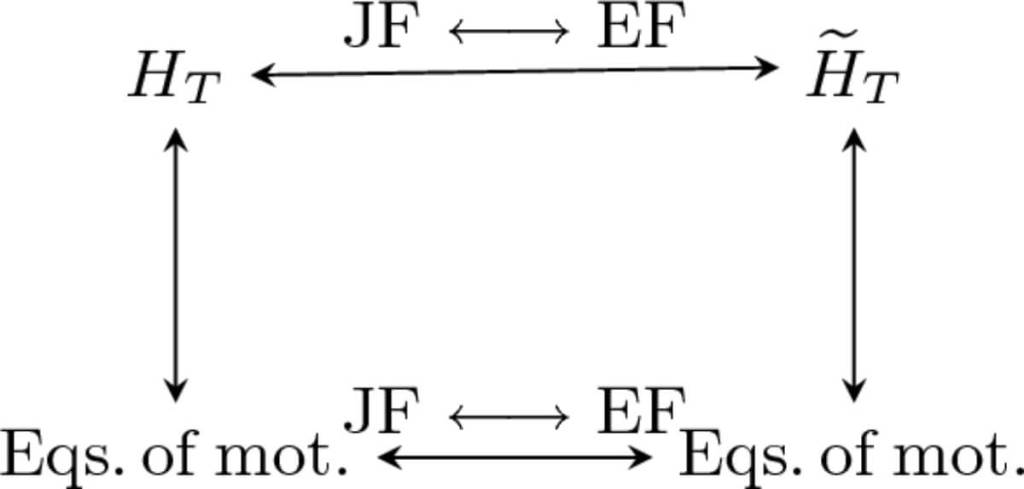
El hallazgo más fascinante del artículo no es simplemente que ambas descripciones puedan ser equivalentes, sino lo que ocurre cuando esa equivalencia se rompe. Esto sucede cuando la transformación matemática que conecta ambos marcos, llamada transformación canónica, se vuelve singular.
En términos sencillos, una transformación singular significa que se rompe la relación directa entre las variables de ambos marcos. En ese punto, emergen nuevas soluciones a las ecuaciones de Einstein, que no existían antes. Estas soluciones incluyen agujeros negros distintos, singularidades “desnudas” y configuraciones espaciales completamente nuevas.
Según el artículo, “la singularidad de la transformación no sólo rompe el vínculo entre los dos marcos, sino que genera universos teóricos completamente nuevos”. No se trata de una exageración retórica: los autores muestran que los resultados son matemáticamente consistentes y potencialmente relevantes para modelos cosmológicos reales.
En otras palabras, el simple hecho de elegir un marco matemático u otro puede influir en los universos que se pueden describir. No se trata solo de una cuestión de lenguaje, sino de realidad física. Lo que parecía un problema abstracto de traducción entre dos sistemas matemáticos se convierte, de pronto, en una puerta abierta a nuevas realidades posibles.
¿Por qué importa este descubrimiento?
Este tipo de investigación puede parecer alejada de la vida cotidiana, pero sus implicaciones son profundas. La forma en que describimos matemáticamente el universo no es neutra, y puede condicionar los fenómenos que podemos predecir o comprender. Esta es una idea que ha sido explorada filosóficamente desde hace siglos, pero aquí se demuestra de manera concreta.
Además, el estudio tiene aplicaciones prácticas. Comprender mejor cómo se comporta la gravedad en presencia de campos escalares es crucial para múltiples áreas de la física actual. Desde la búsqueda de una teoría cuántica de la gravedad hasta los modelos inflacionarios del Big Bang, muchos de los grandes enigmas científicos pasan por ahí.
Este trabajo también muestra cómo la ciencia no siempre avanza por acumulación, sino también corrigiendo errores del pasado. Ignorar los términos de borde era una omisión común en muchos estudios, pero gracias a esta revisión rigurosa, se han podido abrir nuevos caminos.
Referencias
- Gabriele Gionti S.J., Matteo Galaverni. Hamiltonian analysis of scalar-tensor theories: the Jordan and Einstein frame equivalence revisited. The European Physical Journal C (2024). https://doi.org/10.1140/epjc/s10052-024-12260-1.




