La física cuántica a veces da lugar a conceptos tan abstractos que, durante años, parecían condenados a vivir solo en ecuaciones. Pero, como ocurre con frecuencia en ciencia, una idea teórica puede pasar de ser una curiosidad matemática a una herramienta para entender el mundo físico. Uno de estos casos es el de la métrica cuántica, una propiedad de los materiales que no se había observado experimentalmente hasta hace poco.
Un equipo internacional de físicos, liderado desde la Universidad de Ginebra, ha logrado detectar por primera vez esta métrica cuántica en un material real, concretamente en una interfaz de óxidos. Lo interesante no es solo la observación en sí, sino lo que implica: los electrones, al moverse dentro de ciertos materiales, se ven deformados por esta geometría cuántica del mismo modo en que la luz se curva al pasar cerca de una estrella, según predice la relatividad general. El descubrimiento abre la puerta a tecnologías electrónicas basadas en propiedades geométricas fundamentales de la materia, y no simplemente en su composición química.
Qué es la métrica cuántica y por qué importa
En física cuántica, los electrones no son solo partículas, sino también ondas. Esas ondas tienen una forma en el espacio que depende del entorno en el que se mueven. La métrica cuántica es una forma de medir cómo cambian esas ondas cuando se desplazan. Técnicamente, es la parte real del tensor geométrico cuántico y se complementa con otro componente más conocido: la curvatura de Berry, responsable de muchos efectos de transporte electrónico exóticos.
Hasta ahora, se habían identificado fenómenos vinculados a la curvatura de Berry, pero la métrica cuántica era más esquiva. Como explican los autores del estudio, "la métrica cuántica g=Re(G) corresponde a la parte real del tensor geométrico cuántico G" y, junto con la curvatura de Berry, "define las características geométricas y topológicas de los sistemas cuánticos" . Es decir, la forma en la que los electrones sienten y responden al espacio dentro de un material tiene una base geométrica concreta, hasta ahora prácticamente inaccesible.

El sistema experimental: una interfaz con propiedades extraordinarias
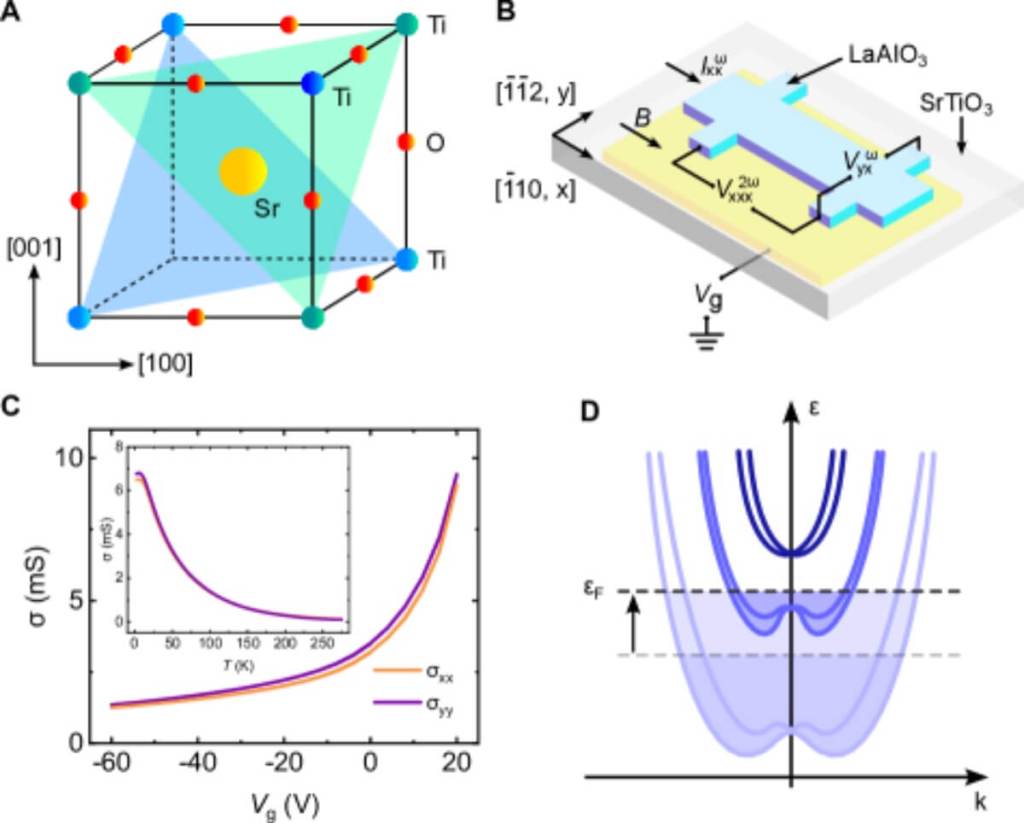
Para observar esta métrica cuántica, los investigadores utilizaron una interfaz entre dos materiales muy conocidos: LaAlO₃ (aluminato de lantano) y SrTiO₃ (titanato de estroncio), colocados en una orientación específica: la (111). En este tipo de heteroestructura se forma un gas electrónico bidimensional con características muy particulares, como el bloqueo espín-momento, es decir, una relación fija entre la dirección del movimiento de los electrones y su espín.
Este bloqueo genera lo que se conoce como efecto Rashba, una división de las bandas electrónicas causada por la interacción entre espín y movimiento. Según el artículo, "el acoplamiento lineal entre el momento cristalino k y el espín electrónico σ conduce a texturas helicoidales de espín", y aunque eso no genera curvatura de Berry, sí da lugar a una métrica cuántica finita.
Gracias a este diseño, y aplicando un campo magnético en el plano del material, los científicos lograron inducir una respuesta electrónica no lineal, un fenómeno que depende directamente de la existencia de la métrica cuántica. A este efecto lo llaman resistencia magnetoeléctrica de la métrica cuántica (QMMR, por sus siglas en inglés).
Un efecto medible: la resistencia no lineal inducida por la geometría
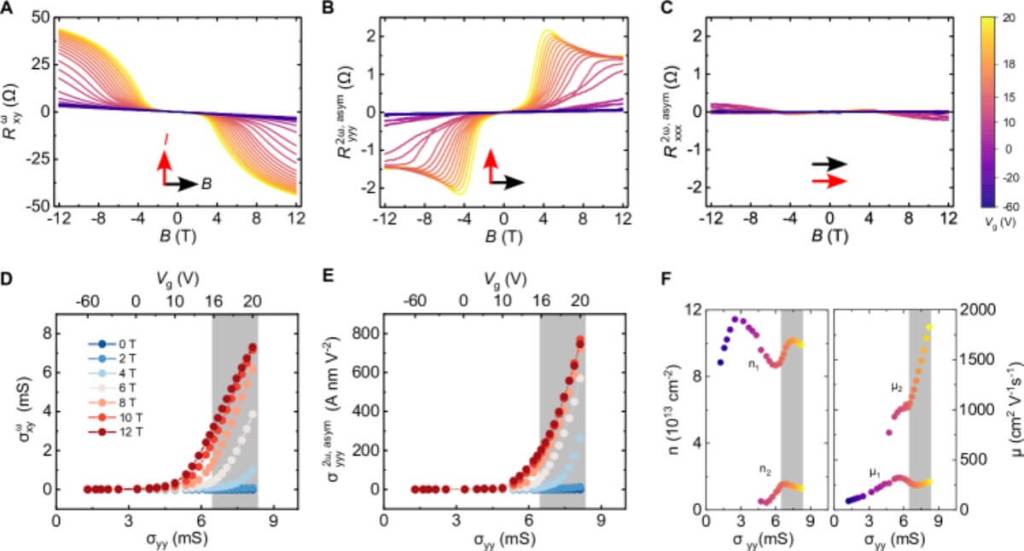
Una de las claves del experimento fue aplicar un campo magnético en el plano del material, lo que rompe la simetría de inversión temporal y permite que la métrica cuántica genere una señal eléctrica observable. Según detallan los autores, "el transporte electrónico asociado a la métrica cuántica se vuelve posible solo al romper la simetría de inversión temporal".
La señal que observaron fue una resistencia longitudinal no lineal y asimétrica respecto al campo magnético, que solo aparece cuando el campo es perpendicular a la dirección de la corriente eléctrica. Esto coincide con las predicciones teóricas, que indican que la componente de dipolo responsable del efecto es nula cuando el campo y la corriente están alineados, pero se vuelve finita cuando están ortogonales.
El resultado es claro: cuando los electrones se desplazan bajo ciertas condiciones, su trayectoria se ve deformada por la geometría interna del espacio cuántico del material, un efecto análogo —aunque no idéntico— al de la gravedad sobre la luz. Esta observación directa marca un antes y un después en el estudio de las propiedades geométricas cuánticas.
La diferencia con materiales topológicos y su ventaja
Hasta ahora, los efectos de la métrica cuántica solo se habían identificado en materiales muy específicos, como ciertos antiferromagnetos topológicos. Pero el estudio demuestra que no es necesario recurrir a sistemas con simetría combinada PT (paridad-tiempo). Como indican en el artículo, "la QMMR está permitida en materiales que carecen de simetría PT".
Esto significa que la métrica cuántica puede manifestarse en materiales mucho más comunes y variados, ampliando enormemente su relevancia experimental y tecnológica. De hecho, los autores sostienen que "la métrica cuántica es una propiedad intrínseca de muchas clases de materiales" , lo que la convierte en una herramienta potencial para múltiples aplicaciones.
La posibilidad de aprovechar este fenómeno en dispositivos semiconductores, metales pesados, interfaces magnéticas e incluso materiales policristalinos multiplica las oportunidades de diseño funcional en el campo de la electrónica cuántica.
Más allá del laboratorio: perspectivas tecnológicas
El hallazgo tiene implicaciones claras para tecnologías emergentes, especialmente en electrónica de alta frecuencia (terahercios), superconductividad y acoplamiento luz–materia. La razón es que la métrica cuántica no solo afecta al transporte de cargas, sino también a cómo los electrones interactúan con otros campos, como los ópticos o magnéticos.
Los autores señalan que integrar este tipo de propiedades con películas ferromagnéticas o ferroeléctricas podría permitir un control reversible y no volátil de los efectos asociados a la geometría cuántica. Esto abriría la puerta a nuevas arquitecturas en computación y detección cuántica, en las que el comportamiento electrónico pueda programarse mediante campos externos, sin necesidad de alterar la estructura del material.
Como resumen, el trabajo demuestra que una propiedad puramente teórica, desarrollada hace dos décadas, puede tener efectos reales, medibles y funcionales en sistemas materiales controlados. Esto no solo valida el valor predictivo de la física teórica, sino que inaugura un nuevo capítulo en el estudio y aprovechamiento de la geometría cuántica.
Referencias
- Sala, G., Mercaldo, M.T., Domi, K., Gariglio, S., Cuoco, M., Ortix, C., & Caviglia, A.D. (2025). The quantum metric of electrons with spin-momentum locking. Science. https://www.science.org/doi/10.1126/science.adq3255




