A primera vista, el principio de equivalencia de Einstein puede parecer contradictorio. Incluso a físicos y matemáticos de formación, les cuesta entender a veces su profundo significado. Aquí será presentado en una versión coloquial, bajo la forma de un Diálogo de Galileo. Apto para no expertos en tan difícil materia.
Situando brevemente a Galileo y a Einstein
A Galileo Galilei (1564–1642) se le sitúa siempre en el origen de la ciencia moderna. En sus famosos Diálogos (Florencia, 1632), se describe por vez primera en la historia el principio de relatividad. Galileo lo hace en el transcurso de una larga conversación entre tres personajes, que tiene lugar durante cuatro jornadas, sobre cómo es nuestro mundo. Salviati (su alter ego), firme defensor de la visión copernicana del sistema solar (por entonces extremadamente revolucionaria), es quien, el segundo día, ilustra el principio de covariancia o de relatividad valiéndose de una plácida navegación por el Arno, el río que cruza la bella Florencia. Simplicio, fiel seguidor de Aristóteles, defiende la versión tolemaica, postula que la Tierra está en el centro del Universo. Y Sagredo, neófito inteligente, busca únicamente la verdad, sin aferrarse a dogma preconcebido alguno; es, de algún modo, el juez de la contienda.
Dando ahora un salto de tres siglos, el descubrimiento más extraordinario de Albert Einstein fue que las masas y el campo gravitatorio pueden hacerse desaparecer, al situarnos en un sistema inercial, siendo entonces reemplazados por la geometría, por la curvatura del espacio-tiempo (Fig. 1). Lo denominó el principio de equivalencia, y en el reside la quintaesencia de su teoría general de la relatividad (TGR); la cual es, de hecho, una teoría del espacio-tiempo.
Vamos a tratar ahora de entender este concepto tan revolucionario y simple, a la vez, en una versión coloquial, casi teatralizada, apta para todo tipo de lectores/as. Lo haremos tomando prestado el formato de los Diálogos de Galileo y a modo de una apasionante discusión científica, que el que esto escribe presenció, de hecho, en un reputadísimo coloquio de una prestigiosa universidad española.

El principio de equivalencia para no expertos
En el turno de preguntas de un importante coloquio, celebrado hace unos meses, sobre los principios fundamentales de la teoría de la relatividad, que un colega mío (le llamaré Salviati, recordando al personaje de Galileo) impartió en un prestigioso instituto matemático (aula expectante, llena a rebosar), fui testigo de cómo era interpelado, de manera poco amable, por uno de los ilustres participantes (llamémosle Simplicio, pues hará honor a ese nombre). De repente, como se apreciará en el apasionante intercambio de ideas que tuvo lugar, me sentí inmerso en una discusión digna de los famosos Diálogos (Fig. 2).
Con insultante suficiencia, Simplicio hizo gala de sus “vastos” conocimientos sobre el tema objetando, con modales autoritarios, que la fuerza de la gravedad nada tenía que ver con las demás fuerzas, dado que es la única que puede ser reducida a geometría del espacio-tiempo. En consecuencia, todo lo que Salviati acababa de afirmar (¡siguiendo al mismísimo Einstein!, puntualizo yo) sobre la equivalencia de todas las fuerzas no se sostenía en absoluto. ¡Era absolutamente contrario a la realidad conocida!
Ese es nuestro Simplicio, en su versión más genuina. Podrá reconocerle enseguida todo aquel que haya leído los Diálogos. Siempre se aferra a lo que le muestran sus ojos: el Sol y el Universo entero giran en torno a la Tierra, día tras otro. Jamás ve más allá. La respuesta de Salviati fue tajante:
“En apariencia, Simplicio lleva razón: la fuerza de la gravedad es muy especial, es de naturaleza muy distinta a la de todas las demás fuerzas. Puede mutar y convertirse ¡en pura geometría! Descubrimiento sublime, para un matemático como él, que quiere llevar la física a su terreno. Pero que, al mismo tiempo, le ciega por completo, y anula cualquier otra consideración que pueda hacerse sobre el tema. Preso de autocomplacencia, queda anclado en lo accesorio, y es del todo incapaz de captar la verdadera esencia, lo fundamental y lo que realmente importa. Que no son aquí las diferencias precisamente, sino lo que todas las fuerzas tienen en común.”
Y dirigiéndose a Sagredo (la audiencia, en este caso), Salviati prosiguió:
“A Simplicio se le escapa que el hecho de que la gravedad sea tan especial no contradice, sino todo lo contrario, refuerza enormemente, si cabe, la importancia del principio de equivalencia, que él, obcecado, se obstina en rechazar:
Pese a ser de naturaleza tan distinta, la gravedad es una fuerza ¡como todas las demás! ¡Ni más ni menos!
Veámoslo acudiendo a un símil muy sencillo, extraído de las lecciones elementales de matemáticas, que todos los aquí presentes habremos recibido sin duda. El número 3 es la clase de equivalencia de todos los conjuntos de 3 elementos, sean estos manzanas, leones o fantasmas [ruego a Simplicio no se ofenda, quizás estoy siendo demasiado trivial ahora], los cuales tienen propiedades muy diversas, pero que conducen al mismo y único concepto matemático: 3.
De igual modo, una fuerza de 3 Newton, ejercida en una dirección determinada, es la misma fuerza, bien sea producida por un asno, una máquina de vapor o una central nuclear. Y Einstein añade: ¡o por la gravedad!, que, como bien afirma Simplicio, ¡parecía ser radicalmente distinta!

Sucede que la fuerza de 3N ejercida por uno u otro ingenio resulta indistinguible para un objeto de masa m, que se acelerará correspondientemente y de forma idéntica en todos los casos: 3N/m. Dicho de otro modo, la masa inercial de todo objeto coincide con su masa gravitatoria, mi = mg (no hay pues aquí dos valores distintos para la masa).
Esta equivalencia tiene su origen y fundamento último en la que Einstein calificó como “la idea más feliz de mi vida”. Un día de 1907, sentado a la mesa de su despacho en la Oficina de Patentes de Berna, le sobresaltó de repente una idea que acababa de cruzar por su mente. Se imaginó, en aquel preciso instante, cayendo de pie desde el tejado de su casa. Y razonó que, si tuviese entonces un objeto en la palma de su mano (una moneda, una manzana), dicho objeto no caería a sus pies, cuando le diese la vuelta a la mano liberándolo: seguiría siempre ¡al lado de su mano! Mientras cayera, Einstein habría eliminado de hecho la fuerza de la gravedad en su entorno inmediato, al colocarse en un sistema acelerado con la misma aceleración que la gravedad. ¡He aquí la esencia de la transformación de la gravedad en geometría!
Lo que conduce aún a otra descripción, en todo análoga, que incluso Simplicio debería ser capaz de entender. Encerremos a un observador en una cápsula situada en el espacio exterior, sin gravedad, y (1) situemos la cápsula sobre un planeta, o (2) en la ingravidez, sometámosla a una fuerza del mismo valor, efectuada por un propulsor que empuja la cápsula hacia arriba, imitando con precisión la gravedad del planeta (Fig. 3). Para el observador dentro de la cápsula, será del todo indistinguible una situación de la otra: nunca podrá saber si es la gravedad o es una fuerza mecánica equivalente lo que le atrae hacia abajo y le permite seguir con su vida habitual.”
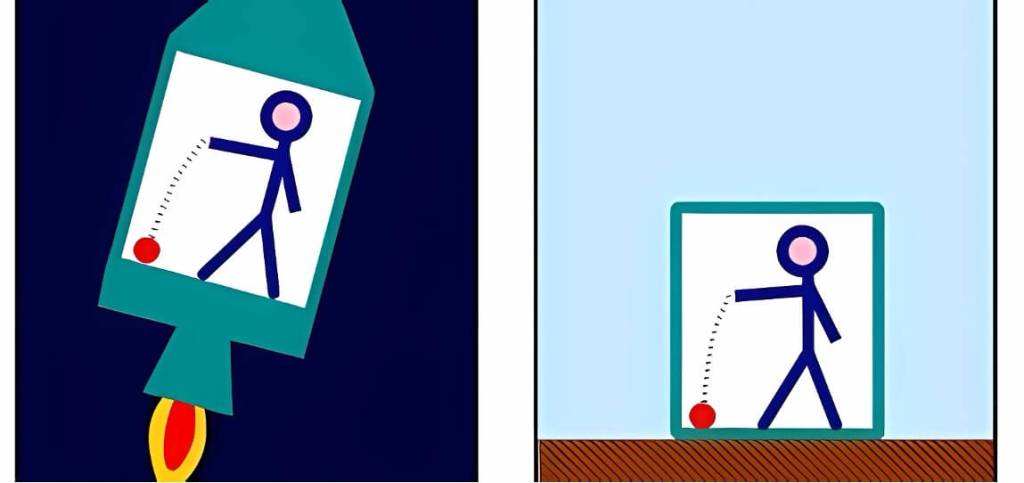
Y Salviati concluyó su detallada respuesta, como sigue: “La gravedad puede ser sustituida por una fuerza mecánica equivalente. Nada tiene de especial como fuerza. Esto es precisamente lo que afirma el principio de equivalencia de Einstein, fundamento de su excepcional TGR. Teoría que se ha demostrado que describe con enorme precisión nuestro Universo, habiendo sido corroborada por un gran número de observaciones y experimentos.”
Simplicio es derrotado. Sagredo (la atenta audiencia, como se ha dicho) estalla en un interminable aplauso, que Salviati agradece emocionado. Para acabar, añade todavía: “Sea como fuere, el verdadero misterio sigue siendo, que de un principio tan elemental emerja una teoría tan sublime. Ya sucedió una vez, con la ley de gravitación universal de Newton, nacida en su jardín cuando, una tarde, mientras contemplaba la Luna vio una manzana caer sobre la hierba.”
Tres observaciones finales relevantes
A todo lo cual es preciso añadir aún tres observaciones, a cual más importante.
- ¿Cómo distinguir a un genio? Acabamos de observar que lo que distingue a un genio es que ve más allá de lo que le muestran sus ojos. Penetra hasta el trasfondo, la propiedad común, la ley fundamental, donde personas como Simplicio solo aprecian los detalles, las diferencias que, aun siendo notables, no vienen a cuento.
- Cabe mencionar, además, al hilo de la respuesta de Salviati, que aquí no termina este caso. Uno de los conceptos más difíciles de la física es la definición de masa, la m que mi colega introdujo alegremente en su ejemplo. Para un bloque de piedra, madera o metal no hay problema; pero sí que aparece cuando hablamos, por ejemplo, de la masa de una estrella de neutrones, o de un agujero negro, un quark o un electrón. Esto nos llevaría muy lejos: a tener que complementar el principio de equivalencia de Einstein con otros más actuales, como el débil y el fuerte. El experimento de Galileo de la Torre de Pisa (si tuvo lugar en realidad) puede ser considerado históricamente como pionero en esa precisa dirección.
- De la ISS, como recinto en caída libre, podemos extraer todavía una última y muy importante lección. Complementa maravillosamente la “idea feliz” de Einstein y nos conduce a entender, de forma cualitativa, sus ecuaciones de la TGR. Hay que tener en cuenta, para empezar, que dentro de la ISS existe todavía una fuerte componente de gravedad terrestre (el 89 % de su valor al nivel del mar) y que, en este caso, la caída libre (ausencia de gravedad) se produce al curvarse la trayectoria (derivadas espaciales de orden dos); esto es, exactamente lo mismo que ocurre con cualquier planeta en su órbita. Tal situación es complementaria a la caída libre imaginada por Einstein desde el tejado de su casa, en la que se tenía aceleración pura (derivada de orden dos respecto al tiempo). Juntando ambas descripciones, se obtiene ya el caso general de las ecuaciones de Einstein, correspondientes a su principio de equivalencia: a la izquierda aparecen las curvaturas y aceleraciones del sistema coordenado (componentes del tensor de curvatura espacio-tiempo, derivadas de segundo orden); a la derecha, todas las masas y energías del universo (de cualquier tipo). La TGR establece su equivalencia, la igualdad estricta de ambos términos: curvatura = energía. ¡Y eso es todo!
Esta fue la exitosa implementación, a orden dos, del ambicioso principio de Ernst Mach, que el propio Einstein confesó (nada más terminar de escribir sus ecuaciones), que no había sido capaz de extender a orden tres ni superiores (movimientos más generales, relatividad total); ver referencias, más abajo. Einstein consideró siempre que la teoría a la que había llegado no era todavía la definitiva, y que alguien la mejoraría pronto. Cosa que todavía no ha ocurrido.
Referencias
- E. Elizalde, The true story of modern cosmology (Springer-Nature, Berlín, 2021).
- E. Elizalde, Cosmología moderna: desde sus orígenes; Catarata, Ed.; Col. Física y Ciencia para todos (Real Sociedad Española de Física y Fundación Ramón Areces): Madrid, 2020.

Emilio Elizalde
Lic. Física, Lic. Matemáticas, Dr. Física
Prof. de Investigación CSIC






