A Pitágoras se le atribuye la afirmación: «Todo es número». Lo que sí sabemos con certeza es que, motivados por cuestiones estéticas y religiosas, los pitagóricos lograron establecer modelos matemáticos de fenómenos físicos, siendo el estudio de la armonía musical uno de sus principales logros. Durante 25 siglos la estela del pitagorismo en la historia del pensamiento científico ha sido brillante y exitosa, explicando el Universo a partir de los números.
Entre luces y sobras
Pitágoras de Samos (ca. 570 a. C. - ca. 490 a. C.) es considerado en numerosas fuentes bibliográficas como el primer matemático puro de la historia de la humanidad. Aunque no se ha conservado ninguno de sus escritos y en sus primeras biografías se le atribuyen poderes divinos, hay bastante acuerdo sobre los principales acontecimientos y logros científicos de su vida, no así sobre las fechas de los mismos, que varían de unas fuentes a otras.
Hijo de un rico comerciante afincado en Samos, próspera ciudad cercana a Mileto, recibió una buena educación. Aprendió a tocar la lira, poesía y recitaba a Homero. Entre sus maestros se citan tres filósofos, su tío materno Ferécides de Siros, Tales y su discípulo Anaximandro, ambos de Mileto y quienes le introdujeron en la geometría, astronomía y las matemáticas. Alrededor del 535 a. C., Pitágoras viajó a Egipto, donde entró en el sacerdocio del templo de Diospolis. Probablemente allí adoptaría buena parte de las creencias que más adelante enseñaría en su propia escuela en Crotona, en la Magna Grecia. Por ejemplo, el secretismo de los sacerdotes, su afán por la pureza o su negativa a vestir con pieles de animales o a comer judías.
En el 525 el rey de Persia invade Egipto y Pitágoras es tomado como prisionero y conducido a Babilonia. Allí es instruido en los ritos sagrados y místicos de los sacerdotes Magoi, completando su formación en aritmética, música y astronomía. Cinco años más tarde consigue regresar a su Samos natal, saliendo unos meses después hacia Crotona, una de las prósperas colonias griegas fundadas en el sur de la Italia actual. Allí Pitágoras se asentó definitivamente y fundó una escuela de pensamiento filosófico-religioso-científíco que ha llegado hasta nosotros, el pitagorismo. Según la RAE, este es el «conjunto de las doctrinas de Pitágoras y sus discípulos, que sostenía el carácter místico de los números, la armonía del universo basada en ellos y la transmigración de las almas».

Tras su larga experiencia en Egipto y Oriente, Pitágoras poseía un sistema de pensamiento más o menos ajustado. En Crotona, sus enseñanzas fueron recibidas con éxito, extendiendo su influencia en esta y otras localidades rápidamente. Proclamaban fundamentalmente la necesidad de ajustar la conducta humana a los cánones de armonía y justicia que se derivaban de la naturaleza. La inmortalidad del alma teñía la vida pitagórica de un profundo carácter religioso y ascético.
La comunidad pitagórica, mitad religiosa y mitad científica, seguía un código secreto y en la terminología de hoy en día, sería calificada de secta, sin matices peyorativos. El maestro, guía y máxima autoridad, ofrecía a sus seguidores una serie de reglas de obligado cumplimiento para caminar por la vida. La comunidad tenía una fuerte estructura jerarquizada con mandos intermedios y unos códigos de ascenso a la verdad. Los miembros del grupo se distinguían por su vestimenta, alimentación y rituales, siendo una forma de vida alternativa a la sociedad establecida. La traición a la comunidad se pagaba con el olvido e incluso la muerte. Según cuenta la leyenda, la revelación del secreto sobre la existencia de números irracionales terminó con el asesinato del pitagórico Hipaso de Metaponto.
El origen de las matemáticas, de religión y música a ciencia
Uno de los descubrimientos matemáticos más importantes de Pitágoras o de sus colaboradores es el celebérrimo teorema que lleva su nombre. La famosa proposición establece la igualdad entre el cuadrado de la hipotenusa y la suma de los cuadrados de los catetos en un triángulo rectángulo. Ya se conocía, en casos particulares, del resultado en culturas anteriores a la griega, como la egipcia y la babilónica e independientemente en la India o China. Los griegos fueron los primeros en demostrar el teorema en el caso general.
Pero si por algo ha trascendido hasta la actualidad el pensamiento pitagórico ha sido por su creencia fundamental de que los números eran la esencia de todas las cosas y que el mundo era armonía. Para ello, Pitágoras y sus discípulos se dedicaron a descubrir propiedades y relaciones numéricas, estableciendo analogías entre los números y la naturaleza. Como resultado de este proceso se creó una mística numérica que influyó en todo el mundo antiguo, y que acabó con la fundación de una nueva ciencia, las Matemáticas.
Las propiedades matemáticas de los números fascinaron a los pitagóricos, que edificaron sus creencias religiosas-filosóficas sobre ellas. Estudiaron los números triangulares, cuadrados, pentagonales o piramidales, en ocasiones con guijarros para realizar las figuras que les daban nombre. Fórmulas como 1+3+5+ ….+2n-1= n2 , que muestra que los cuadrados pueden descomponerse como suma de números impares, les parecían una pura expresión de lo divino.
Pero fue a través de la profunda conexión entre la música y las matemáticas donde los pitagóricos afianzaron sus creencias místicas en el poder matemático de la naturaleza. Cuenta la leyenda que una mañana, al pasar Pitágoras cerca de una herrería, comprobó que los sonidos que emitían varios martillos de diferentes tamaños al golpear láminas de diversas longitudes eran armoniosos. Esto le llevo a plantearse cuál era la causa por la que dos notas diferentes sonaran bien al oído cuando se tocasen a la vez o por el contrario sonasen disonantes.
Se le atribuye el diseño del monocordio (instrumento musical de una cuerda) que permitía variar fácilmente su longitud. Al dividir la longitud de la cuerda por 2, la frecuencia del sonido emitido, denotémosla por f, se duplica y el nuevo sonido está en consonancia con el inicial. La sensación percibida es que ambos sonidos son la misma nota, pero la segunda más aguda que la primera. Se dice que ambas notas están a distancia de una octava.
Estamos ahora interesados en rellenar el espacio de una octava entre f y 2f con otras notas consonantes. Lo lógico es seguir con fracciones sencillas y reducir la distancia de la cuerda en 2/3 de la inicial, esto es, multiplicar nuestra frecuencia por 3/2, obteniendo una nueva nota agradable de frecuencia (3/2)f y llamada quinta de f. Si repetimos el proceso obtendríamos un nota de frecuencia (9/4)f, mayor que 2f, y que se reduce a (9/8)f, dividiendo por 2 (bajarla una octava). Reiteramos este proceso dos veces más, ordenamos las frecuencias obtenidas y aproximamos los cocientes de las frecuencias consecutivas como se indica en la siguiente tabla.
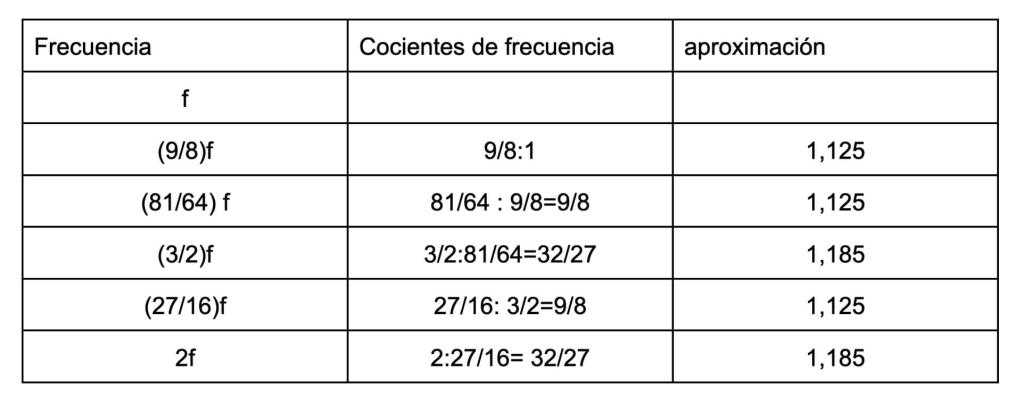
Estas cinco notas forman la llamada escala pentatónica. Aunque parece ser que ya era conocida siglos antes de Pitágoras y su escuela, fue este quien realizó un estudio sistemático y explicó su armonía basándose en las matemáticas.
El tratamiento pitagórico de la música ha llegado hasta la actualidad. Sobre las escalas diatónicas y cromáticas, mejoras de la pentatónica, se ha edificado gran parte de la música occidental. Hoy en día se usa una modificación de esta última, la escala temperada, que distribuye equidistantemente las doce notas en una octava. Los múltiplos perfectos de las frecuencias de la escala diatónica se han perdido, las armonías no son tan redondas (con el consiguiente malestar de los más puristas) pero, a cambio, se simplifica la tarea de afinación de los instrumentos musicales.
El pitagorismo después de los pitagóricos: Da Vinci, Kepler, Galileo, Newton, Einstein…
Las relaciones numéricas entre las notas musicales consonantes llevaron a los pitagóricos a pensar que del mismo modo debían existir otras relaciones numéricas análogas que gobernaran el universo armonioso en el que vivimos, como por ejemplo, el movimiento majestuoso de los astros.
Tras casi dos mil años, la llegada del Renacimiento supuso un redescubrimiento de los clásicos, en particular de la tradición griega matemática y de sus orígenes en la escuela pitagórica. El Tratado de la Pintura de Leonardo da Vinci (1452-1519), contiene la siguiente reflexión: «Ninguna investigación humana se puede demostrar verdadera ciencia, si ella no pasa por las demostraciones matemáticas». El matemático y astrónomo alemán Johannes Kepler (1571-1630) defendía esa filosofía pitagórica, creyendo en los números como la esencia de la naturaleza y de Dios. En su libro en Mysterium Cosmigraphicum (1597) Kepler escribía «La Geometría es uno de los eternos reflejos de la mente de Dios».
En Il Saggiatore (1623) Galileo expone por primera vez las bases del método científico, que usamos hoy en día: combinación de observación, formulación matemática y experimentación. Además escribe la siguiente afirmación sobre el universo, de inspiración claramente pitagórico: «La filosofía [natural] está escrita en ese grandioso libro que tenemos abierto ante los ojos, (quiero decir, el universo), pero no se puede entender si antes no se aprende a entender la lengua, a conocer los caracteres en los que está escrito. Está escrito en lengua matemática y sus caracteres son triángulos, círculos y otras figuras geométricas, sin las cuales es imposible entender ni una palabra; sin ellos es como girar vanamente en un oscuro laberinto».

Con Philosophiae naturalis principia mathematica (1687), Isaac Newton (1642- 1727) consigue por vez primera construir un modelo matemático general que permite explicar tanto los movimientos de los cuerpos celestes como de los terrestres, enunciando la ley de gravitación universal. Citando a Kepler y Galileo, afirma: «Los últimos autores, como los más antiguos, se esforzaron por subordinar los fenómenos de la naturaleza a las leyes de las matemáticas».
En 1796 Pierre-Simon Laplace (1749-1827) publica su Exposition du système du monde en la que conjeturó la formación del Sol y del Sistema Solar a partir de una nebulosa, probó la estabilidad del Sistema Solar y defendió su fe en un mundo determinista, afirmando: «Todos los fenómenos de la naturaleza son solo los resultados matemáticos de un pequeño número de leyes inmutables».
El gran físico del siglo xx, Albert Einstein (1879-1955), pronunció la conferencia Herbert Spencer en la primavera de 1933 en Oxford donde lanzó las siguientes reflexiones: «La experiencia puede sugerir los conceptos matemáticos apropiados, pero estos, sin duda ninguna, no pueden ser deducidos de ella.
Por supuesto que la experiencia retiene su cualidad de criterio último de la utilidad física de una construcción matemática. Pero el principio creativo reside en la matemática. Por tanto, en cierto sentido, considero que el pensamiento puro puede captar la realidad, tal como los antiguos habían soñado». En el libro del año 2015 Nuestro universo matemático: En busca de la naturaleza última de la realidad, el cosmólogo y profesor del Instituto Tecnológico de Massachusetts Max Tegmark da un paso más allá en el pitagorismo al proponer que nuestro mundo físico no solo puede ser descrito por las matemáticas, sino que «es» matemáticas.
Así afirma que nuestra realidad física externa es una estructura matemática en sí misma y en aquellos universos lo suficientemente complejos que contienen subestructuras autoconscientes (nosotros mismos) se da el fenómeno de que son capaces de percibir el mundo real físico como un entorno holográfico (recordando la película de Matrix).
En estas hipótesis el multiverso serían todos los mundos posibles donde todas las verdades lógicas, ecuaciones, constantes, y teoremas matemáticos computables (en sentido de Gödel) existen por necesidad lógica.
Sin llegar a los extremos de la teoría de Max Tegmark, podemos estar seguros de la importancia histórica y científica de Pitágoras de Samos. Para corroborar esta idea nos sirve la afirmación del matemático, filósofo y premio Nobel de Literatura, el británico Bertrand Russell (1872-1970) en su Historia de la Filosofía Universal: «No conozco ningún otro hombre que haya tenido mayor influencia en el campo del pensamiento, porque lo que aparece como platonismo resulta después de analizarlo, esencialmente pitagorismo».




