Una ecuación es una igualdad matemática formada por dos expresiones que contienen una o más incógnitas que pueden despejarse (resolverse) a través de una sucesión de operaciones matemáticas. Dicho así, habrá muchos que levanten una ceja en señal de incomprensión o duda y maldigan para sus adentros ese antiguo enemigo de la época escolar que son las matemáticas. Esta es, probablemente, una de las ciencias formales más incomprendidas por la sociedad y sin embargo más básicas para comprender el mundo que nos rodea y el universo en que habitamos. Las matemáticas son el engranaje central que hace que giren todos los demás elementos que forman el cosmos. Así lo demuestra esta serie de ecuaciones históricas, que te ayudarán a entender distintos fenómenos.
Importancia de las matemáticas en el mundo: ecuaciones históricas
Las matemáticas son el lenguaje universal que permite describir y entender el mundo. Sin ellas, sería imposible avanzar en campos como la física, la química, la ingeniería, la medicina y las ciencias sociales. Las ecuaciones matemáticas son la herramienta que nos permite formular leyes y modelos que explican fenómenos naturales y artificiales. Desde la estructura del ADN hasta las órbitas planetarias, todo puede ser descrito mediante ecuaciones, lo que subraya su importancia en el conocimiento humano.
En la vida cotidiana, las matemáticas son omnipresentes. Desde el simple acto de medir ingredientes en la cocina hasta las complejas transacciones financieras, las ecuaciones facilitan la realización de tareas diarias. Además, las matemáticas nos permiten entender conceptos abstractos como el tiempo, el espacio y la energía, lo que nos ayuda a comprender mejor el universo en el que vivimos. La capacidad de predecir fenómenos naturales y tecnológicos se basa en modelos matemáticos que han sido desarrollados a lo largo de siglos.
El impacto de las matemáticas trasciende los límites de la ciencia. En el ámbito social, las ecuaciones son herramientas cruciales para el análisis de datos y la toma de decisiones. En economía, por ejemplo, se utilizan para modelar el comportamiento de mercados y prever tendencias. En medicina, ayudan a interpretar datos clínicos y a desarrollar tratamientos. Así, las matemáticas son un motor de innovación y progreso en múltiples áreas de la vida humana.

Teorema de Pitágoras: La base de la geometría
El teorema de Pitágoras es una de las ecuaciones históricas de la geometría, y una de las primeras ecuaciones históricas formuladas. Pitágoras en el siglo VI a.C., establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. Esta relación no solo es esencial para la geometría, sino que también conecta el álgebra con la geometría, permitiendo resolver problemas complejos con mayor facilidad. Su aplicación se extiende desde la arquitectura hasta la navegación, demostrando su relevancia en múltiples campos.
La simplicidad del teorema de Pitágoras es engañosa, ya que sus implicaciones son profundas. Permite calcular distancias y ángulos en el espacio tridimensional, lo que es vital para disciplinas como la ingeniería y la física. Además, este teorema es la base para el desarrollo de conceptos más avanzados en matemáticas, como la trigonometría y el cálculo diferencial. Su influencia se siente en cada rincón de la ciencia y la tecnología modernas.
En la educación, el teorema de Pitágoras es una de las primeras ecuaciones que se enseñan, debido a su importancia y aplicabilidad. Los estudiantes aprenden a utilizarlo para resolver problemas prácticos, lo que les proporciona una comprensión más profunda de la geometría. Esta ecuación ha resistido la prueba del tiempo, y su legado sigue siendo una parte integral del currículo matemático en todo el mundo.
Logaritmos: Simplificación de cálculos complejos
Los logaritmos, introducidos por John Napier en el siglo XVII, revolucionaron la forma en que se realizaban los cálculos matemáticos. Antes de la invención de las calculadoras y ordenadores, los logaritmos permitieron simplificar operaciones complejas, como la multiplicación y la división, convirtiéndolas en sumas y restas más manejables. Esta innovación fue crucial para el avance de la astronomía, la navegación y la ingeniería, donde los cálculos precisos son esenciales.
El uso de logaritmos facilitó el desarrollo de tablas logarítmicas, que fueron herramientas indispensables para científicos e ingenieros durante siglos. Estas tablas permitieron realizar cálculos con gran precisión, lo que fue fundamental para el progreso de la ciencia y la tecnología. Además, los logaritmos sentaron las bases para el desarrollo de otras áreas matemáticas, como la teoría de números y la estadística.
En la actualidad, los logaritmos siguen siendo una herramienta valiosa en múltiples disciplinas. En informática, por ejemplo, se utilizan para analizar algoritmos y optimizar procesos. En finanzas, ayudan a modelar el crecimiento exponencial y a calcular tasas de interés. Así, los logaritmos continúan siendo una parte esencial de las matemáticas aplicadas, demostrando su perdurable relevancia. Muchas de las ecuaciones históricas más importantes tienen un componente logarítmico.
Cálculo: Comprendiendo el cambio de funciones
El cálculo, desarrollado por Isaac Newton y Gottfried Wilhelm Leibniz en el siglo XVII, es una rama fundamental de las matemáticas que permite comprender el cambio y el movimiento. La definición de la derivada, una de las bases del cálculo, permite analizar cómo cambian las funciones cuando sus variables se modifican. Esto es esencial para entender fenómenos dinámicos en la física, la ingeniería y la economía, donde el cambio es una constante. Para explicar estos fenómenos, varios científicos a lo largo de la historia formularon sus propias teorías, hasta convertirlas en ecuaciones históricas.
El cálculo diferencial e integral ha permitido resolver problemas complejos en una amplia gama de campos. En física, por ejemplo, es crucial para describir el movimiento de los cuerpos y las leyes de la naturaleza. En economía, ayuda a modelar el comportamiento de los mercados y a optimizar recursos. La capacidad de predecir y controlar el cambio es una de las razones por las que el cálculo es tan valioso.
La enseñanza del cálculo es un componente esencial de la educación matemática. Los estudiantes aprenden a utilizarlo para resolver problemas prácticos y teóricos, lo que les proporciona una comprensión más profunda de las matemáticas. A medida que avanzan en sus estudios, descubren que el cálculo es una herramienta poderosa que les permite abordar problemas complejos con confianza y precisión.
Ley de la gravedad: La descripción universal de Newton
La ley de la gravedad, formulada por Isaac Newton en 1687, es una de las ecuaciones históricas más influyentes. Esta ley describe cómo dos cuerpos se atraen mutuamente con una fuerza proporcional a sus masas e inversamente proporcional al cuadrado de la distancia que los separa. La comprensión de este fenómeno permitió explicar desde la caída de una manzana hasta las órbitas de los planetas, unificando fenómenos aparentemente dispares bajo una sola teoría.
La formulación de la ley de la gravedad fue un hito en la historia de la ciencia, ya que proporcionó una explicación coherente del movimiento celestial. Antes de Newton, las teorías sobre el movimiento de los cuerpos celestes eran fragmentarias y poco precisas. La ley de la gravedad permitió predecir con exactitud las trayectorias de los planetas y los cometas, lo que fue fundamental para el desarrollo de la astronomía moderna.

Además de su impacto en la astronomía, la ley de la gravedad ha tenido aplicaciones prácticas en la ingeniería y la tecnología. Desde el diseño de puentes y edificios hasta la planificación de misiones espaciales, esta ecuación es una herramienta esencial para los ingenieros y científicos. Su influencia se extiende a casi todos los aspectos de la vida moderna, demostrando su relevancia continua.
Raíz cuadrada de -1: Números complejos de Euler
La introducción de la raíz cuadrada de -1 por Leonhard Euler en el siglo XVIII marcó el nacimiento de los números complejos, una extensión fundamental del sistema numérico. Estos números, representados como a + bi, donde i es la raíz cuadrada de -1, permiten resolver ecuaciones que no tienen soluciones en el conjunto de los números reales. Los números complejos son esenciales en diversas áreas de la ciencia y la ingeniería, donde se utilizan para modelar fenómenos que no pueden ser descritos únicamente con números reales.
La aparición de los números complejos revolucionó el análisis matemático, permitiendo resolver problemas que antes eran considerados insolubles. En ingeniería eléctrica, por ejemplo, los números complejos son fundamentales para el análisis de circuitos de corriente alterna. En física cuántica, describen el comportamiento de las partículas subatómicas. Así, los números complejos han ampliado el alcance de las matemáticas y han abierto nuevas áreas de investigación.
En el ámbito educativo, los números complejos son un tema avanzado que se introduce en cursos de álgebra y cálculo. Los estudiantes aprenden a operar con ellos y a utilizarlos para resolver problemas complejos. A medida que avanzan en sus estudios, descubren que los números complejos son una herramienta poderosa que les permite abordar problemas matemáticos y científicos con mayor profundidad. Por tanto, se ha demostrado como una de las ecuaciones históricas con mayores aplicaciones.
Fórmula de los poliedros: La topología de Euler
La fórmula de los poliedros, descubierta por Leonhard Euler en el siglo XVIII, es un resultado fundamental en la topología, una rama de las matemáticas que estudia las propiedades de los espacios que permanecen invariantes bajo deformaciones continuas. La fórmula establece que para cualquier poliedro convexo, el número de vértices (V), aristas (A) y caras (C) está relacionado por la ecuación V - A + C = 2. Esta relación es esencial para entender la estructura y la forma de los objetos tridimensionales.
La fórmula de los poliedros ha tenido un impacto significativo en la geometría y la topología, proporcionando una herramienta para clasificar y estudiar las propiedades de los poliedros. Además, ha inspirado el desarrollo de la teoría de grafos, que tiene aplicaciones en informática, biología y redes sociales. La capacidad de analizar y comprender la estructura de los objetos ha sido fundamental para el avance de la ciencia y la tecnología.
En la educación, la fórmula de los poliedros es un tema que se introduce en cursos de geometría y topología. Los estudiantes aprenden a utilizarla para resolver problemas relacionados con la estructura y la forma de los objetos. A medida que avanzan en sus estudios, descubren que esta fórmula es una herramienta valiosa que les permite explorar el mundo tridimensional con mayor profundidad.
Distribución normal: Fundamento estadístico
La distribución normal, también conocida como la campana de Gauss, es una de las distribuciones de probabilidad más importantes en estadística. Formulada por Carl Friedrich Gauss en el siglo XIX, esta distribución describe cómo se distribuyen los datos en torno a una media. Es fundamental para el análisis estadístico, ya que muchos fenómenos naturales y sociales siguen una distribución normal, lo que permite realizar inferencias y predicciones precisas. Esta es una de las ecuaciones históricas de la estadística y las matemáticas.
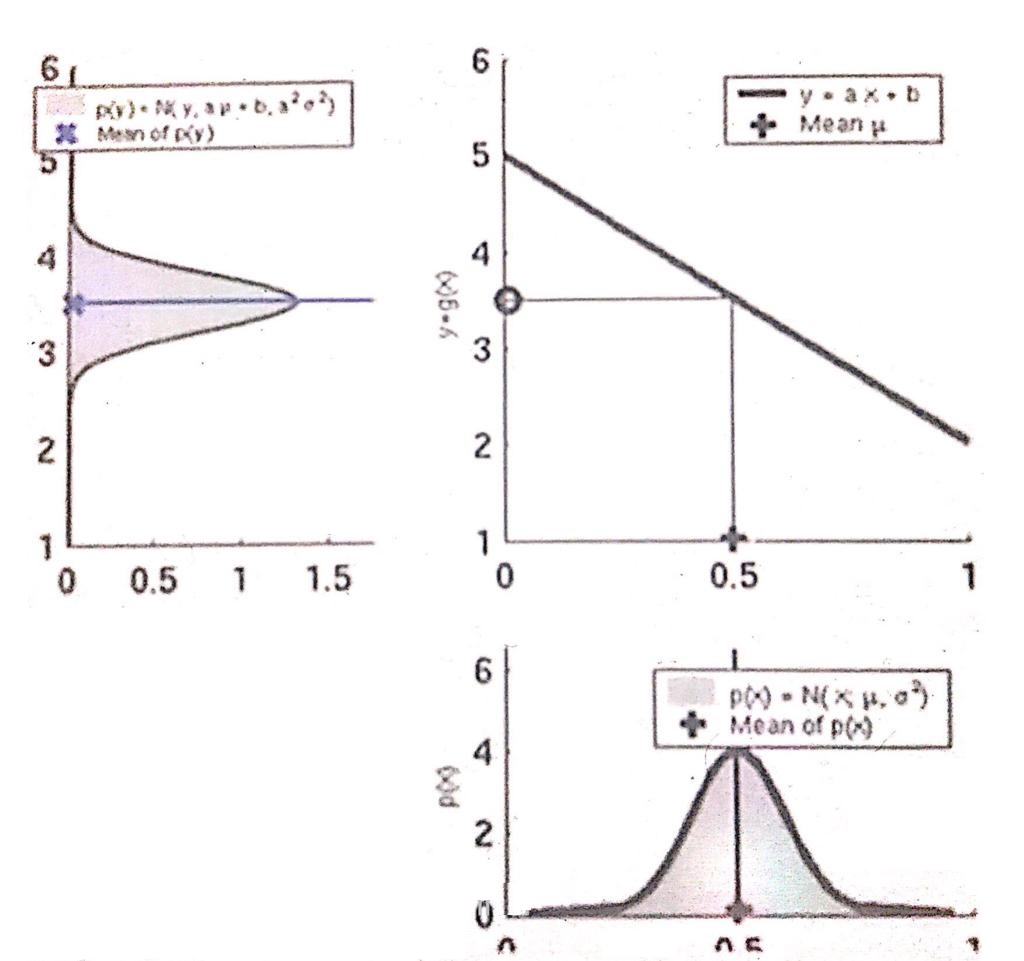
La distribución normal es esencial para la teoría de la probabilidad y la inferencia estadística. Permite modelar la variabilidad de los datos y realizar pruebas de hipótesis, lo que es crucial para la investigación científica y la toma de decisiones. Además, la distribución normal es la base para el desarrollo de otras distribuciones estadísticas, como la distribución t y la chi-cuadrado, que tienen aplicaciones en diversos campos.
En la educación, la distribución normal es un tema central en cursos de estadística y probabilidad. Los estudiantes aprenden a utilizarla para analizar datos y realizar inferencias estadísticas. A medida que avanzan en sus estudios, descubren que la distribución normal es una herramienta poderosa que les permite comprender y modelar la variabilidad de los datos en el mundo real.
Ecuación de onda: La propagación de fenómenos ondulatorios
La ecuación de onda, formulada por Jean le Rond d'Alembert en el siglo XVIII, es una ecuación diferencial que describe cómo se propagan las ondas en un medio. Esta ecuación es fundamental para entender fenómenos ondulatorios como el sonido, la luz y las ondas en el agua. Su aplicación se extiende a campos como el electromagnetismo, la acústica y la dinámica de fluidos, donde es esencial para modelar y predecir el comportamiento de las ondas.
La ecuación de onda ha sido crucial para el desarrollo de la teoría de ondas y ha permitido unificar fenómenos que, a primera vista, parecen dispares. En el electromagnetismo, por ejemplo, la ecuación de onda describe cómo se propagan las ondas electromagnéticas, lo que es fundamental para la transmisión de señales de radio y televisión. En acústica, permite modelar el comportamiento del sonido en diferentes medios, lo que es esencial para el diseño de auditorios y sistemas de sonido.
En la educación, la ecuación de onda es un tema avanzado que se introduce en cursos de física y matemáticas. Los estudiantes aprenden a utilizarla para resolver problemas relacionados con la propagación de ondas. A medida que avanzan en sus estudios, descubren que esta ecuación es una herramienta poderosa que les permite comprender y modelar fenómenos ondulatorios con mayor precisión.
Transformada de Fourier: Descomposición de estructuras complejas
La transformada de Fourier, formulada por Jean-Baptiste Joseph Fourier en el siglo XIX, es una herramienta matemática que permite descomponer una función en sus componentes de frecuencia. Esta técnica es esencial para el análisis de señales y el procesamiento de datos, ya que permite identificar y aislar patrones en datos complejos. Su aplicación se extiende a campos como la ingeniería, la física y la informática, donde es fundamental para el análisis y la síntesis de señales.
La transformada de Fourier ha revolucionado la forma en que se procesan y analizan las señales. En ingeniería, por ejemplo, es crucial para el diseño de sistemas de comunicaciones y el análisis de circuitos. En física, permite estudiar fenómenos periódicos y analizar espectros de frecuencia. Además, la transformada de Fourier es la base para el desarrollo de otras técnicas de análisis de señales, como la transformada de Laplace y la transformada wavelet.
En la educación, la transformada de Fourier es un tema avanzado que se introduce en cursos de matemáticas y ciencias de la computación. Los estudiantes aprenden a utilizarla para analizar y procesar señales. A medida que avanzan en sus estudios, descubren que esta técnica es una herramienta poderosa que les permite descomponer y comprender estructuras complejas con mayor profundidad.
Ecuaciones de Navier-Stokes: Mecánica de fluidos en ingeniería
Las ecuaciones históricas de Navier-Stokes, formuladas por Claude-Louis Navier y George Gabriel Stokes en el siglo XIX, son un conjunto de ecuaciones diferenciales que describen el movimiento de los fluidos. Ecuaciones históricas para la mecánica de fluidos, un campo de la ingeniería que estudia el comportamiento de líquidos y gases en movimiento. Su aplicación es esencial para el diseño de aviones, barcos y sistemas de tuberías, donde es crucial predecir y controlar el flujo de fluidos.
Las ecuaciones de Navier-Stokes han sido históricas para el desarrollo de la aerodinámica y la hidrodinámica, permitiendo modelar y predecir el comportamiento de los fluidos en diferentes condiciones. En la ingeniería aeroespacial, por ejemplo, son esenciales para el diseño de alas y fuselajes de aviones. En la industria petrolera, permiten optimizar el transporte de petróleo y gas a través de tuberías. Así, estas ecuaciones son una herramienta esencial para la ingeniería moderna.
En la educación, las ecuaciones de Navier-Stokes son un tema avanzado que se introduce en cursos de ingeniería y física. Los estudiantes aprenden a utilizarlas para resolver problemas relacionados con el flujo de fluidos. A medida que avanzan en sus estudios, descubren que estas ecuaciones son una herramienta poderosa que les permite comprender y modelar el comportamiento de los fluidos con mayor precisión.
Ecuaciones de Maxwell: Fenómenos electromagnéticos unificados
Las ecuaciones de Maxwell, formuladas por James Clerk Maxwell en el siglo XIX, son un conjunto de ecuaciones históricas que describen el comportamiento del electromagnetismo. Estas ecuaciones unifican los fenómenos eléctricos y magnéticos, proporcionando una comprensión completa de cómo interactúan la electricidad y el magnetismo. Su aplicación es esencial para el desarrollo de tecnologías como la radio, la televisión y la telefonía móvil, donde es crucial transmitir y recibir señales electromagnéticas.
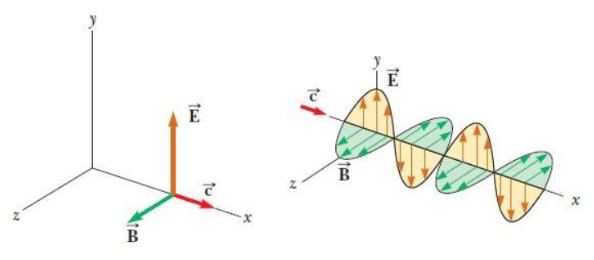
Las ecuaciones de Maxwell han sido cruciales para el desarrollo de la teoría electromagnética, permitiendo predecir y modelar el comportamiento de los campos eléctricos y magnéticos. En la ingeniería eléctrica, por ejemplo, son esenciales para el diseño de circuitos y sistemas de transmisión de energía. En la física, permiten estudiar la propagación de ondas electromagnéticas y analizar espectros de frecuencia. Así, estas ecuaciones son una herramienta esencial para la ciencia y la tecnología modernas.
En la educación, las ecuaciones de Maxwell son un tema avanzado que se introduce en cursos de física y ingeniería. Los estudiantes aprenden a utilizarlas para resolver problemas relacionados con el electromagnetismo. A medida que avanzan en sus estudios, descubren que estas ecuaciones son una herramienta poderosa que les permite comprender y modelar los fenómenos electromagnéticos con mayor precisión.
Segunda ley de la termodinámica: Entropía y equilibrio térmico
La segunda ley de la termodinámica, formulada por Ludwig Boltzmann en el siglo XIX, es una de las leyes más fundamentales de la física. Esta ley establece que en un sistema cerrado, la entropía, una medida del desorden, tiende a aumentar con el tiempo. La comprensión de este principio es esencial para el estudio del equilibrio térmico y la transferencia de calor, donde es crucial predecir y controlar el flujo de energía.
La segunda ley de la termodinámica ha sido crucial para el desarrollo de la termodinámica y la física estadística, permitiendo modelar y predecir el comportamiento de los sistemas termodinámicos. En la ingeniería, por ejemplo, es esencial para el diseño de motores y sistemas de refrigeración. En la física, permite estudiar la transferencia de calor y analizar procesos irreversibles. Así, esta ley es una herramienta esencial para la ciencia y la tecnología modernas.
En la educación, la segunda ley de la termodinámica es un tema central en cursos de física y química. Los estudiantes aprenden a utilizarla para resolver problemas relacionados con la transferencia de calor y el equilibrio térmico. A medida que avanzan en sus estudios, descubren que esta ley es una herramienta poderosa que les permite comprender y modelar el comportamiento de los sistemas termodinámicos con mayor precisión.
Teoría de la relatividad: Einstein y la relación masa-energía
La teoría de la relatividad, formulada por Albert Einstein en el siglo XX, es una de las teorías históricas más indicutibles de la física moderna. Esta teoría establece que la masa y la energía son equivalentes, y que el tiempo y el espacio son relativos y dependen del observador. La comprensión de estos principios ha cambiado radicalmente nuestra visión del universo, permitiendo explicar fenómenos como la dilatación temporal y la curvatura del espacio-tiempo.
La teoría de la relatividad ha sido crucial para el desarrollo de la cosmología y la física de partículas, permitiendo modelar y predecir el comportamiento del universo a gran escala. En la astronomía, por ejemplo, es esencial para el estudio de los agujeros negros y la expansión del universo. En la física de partículas, permite analizar las colisiones de partículas y estudiar las interacciones fundamentales. Así, esta teoría es una herramienta esencial para la ciencia y la tecnología modernas.
En la educación, la teoría de la relatividad es un tema avanzado que se introduce en cursos de física y cosmología. Los estudiantes aprenden a utilizarla para resolver problemas relacionados con el tiempo y el espacio. A medida que avanzan en sus estudios, descubren que esta teoría es una herramienta poderosa que les permite comprender y modelar el comportamiento del universo con mayor profundidad.

Ecuación de Schrödinger: Dinámica cuántica de partículas
La ecuación de Schrödinger, formulada por Erwin Schrödinger en el siglo XX, es una ecuación fundamental de la mecánica cuántica que describe cómo evoluciona el estado cuántico de un sistema con el tiempo. Esta ecuación es esencial para entender el comportamiento de las partículas subatómicas, donde las leyes de la mecánica clásica no son aplicables. Su aplicación es crucial para el desarrollo de tecnologías como la computación cuántica y la criptografía cuántica, donde es fundamental modelar y predecir el comportamiento de los sistemas cuánticos.
La ecuación de Schrödinger ha sido crucial para el desarrollo de la teoría cuántica, permitiendo modelar y predecir el comportamiento de los sistemas cuánticos. En la física, por ejemplo, es esencial para el estudio de los átomos y las moléculas. En la química, permite analizar las reacciones químicas y estudiar las propiedades de los materiales. Así, esta es una de las ecuaciones históricas para la ciencia y la tecnología modernas.

En la educación, la ecuación de Schrödinger es un tema avanzado que se introduce en cursos de física cuántica y química. Los estudiantes aprenden a utilizarla para resolver problemas relacionados con la dinámica cuántica. A medida que avanzan en sus estudios, descubren que esta ecuación es una herramienta poderosa que les permite comprender y modelar el comportamiento de los sistemas cuánticos con mayor precisión.
Teoría de la información: Comunicación y compresión de datos>
La teoría de la información, formulada por Claude Shannon en el siglo XX, es una teoría matemática que describe cómo se mide y transmite la información. Esta teoría, histórica para el desarrollo de las telecomunicaciones y la informática, es crucial para optimizar la transmisión y el almacenamiento de datos. Su aplicación se extiende a campos como la criptografía, la compresión de datos y la teoría de códigos, donde es fundamental garantizar la seguridad y la eficiencia de la comunicación.
La teoría de la información, histórica para el desarrollo de la tecnología digital, permite modelar y optimizar la transmisión de datos. En la informática, por ejemplo, es esencial para el diseño de algoritmos de compresión y la optimización de redes de comunicación. En la criptografía, permite analizar la seguridad de los sistemas de cifrado y garantizar la privacidad de la información. Así, esta teoría es una herramienta esencial para la ciencia y la tecnología modernas.
En la educación, la teoría de la información es un tema avanzado que se introduce en cursos de informática y telecomunicaciones. Los estudiantes aprenden a utilizarla para resolver problemas relacionados con la comunicación y la compresión de datos. A medida que avanzan en sus estudios, descubren que esta teoría es una herramienta poderosa que les permite comprender y modelar el flujo de información con mayor profundidad.
Teoría del caos: Sistemas dinámicos y efecto mariposa
La teoría del caos, desarrollada por Robert May en el siglo XX, es una rama de las matemáticas que estudia el comportamiento de los sistemas dinámicos que son altamente sensibles a las condiciones iniciales. Este fenómeno, conocido como el efecto mariposa, describe cómo pequeñas variaciones en las condiciones iniciales pueden llevar a resultados drásticamente diferentes. La comprensión de estos principios es esencial para el estudio de sistemas complejos en la física, la biología y la economía, donde es crucial predecir y controlar el comportamiento de los sistemas dinámicos.
La teoría del caos es histórica para el desarrollo de la teoría de sistemas complejos, permitiendo modelar y predecir el comportamiento de los sistemas dinámicos. En la meteorología, por ejemplo, es esencial para el estudio del clima y la predicción del tiempo. En la biología, permite analizar la dinámica de poblaciones y estudiar la evolución de los ecosistemas. Así, esta teoría es una herramienta esencial para la ciencia y la tecnología modernas.
En la educación, la teoría del caos es un tema avanzado que se introduce en cursos de matemáticas y ciencia de sistemas. Los estudiantes aprenden a utilizarla para resolver problemas relacionados con los sistemas dinámicos. A medida que avanzan en sus estudios, descubren que esta teoría es una herramienta poderosa que les permite comprender y modelar el comportamiento de los sistemas complejos con mayor precisión.

Ecuación de Black-Scholes: Finanzas y valoración de derivados
La ecuación de Black-Scholes, formulada por Fisher Black y Myron Scholes en el siglo XX, es una ecuación que describe cómo se valoran los derivados financieros, como las opciones. Ecuaciones históricas para el desarrollo de la teoría financiera, donde es crucial modelar y predecir el comportamiento de los mercados. Su aplicación es fundamental para el diseño de estrategias de inversión y la gestión de riesgos, donde es esencial optimizar el rendimiento y minimizar las pérdidas.
La ecuación de Black-Scholes ha sido crucial para el desarrollo de la teoría de las finanzas, permitiendo modelar y predecir el comportamiento de los mercados financieros. En la banca, por ejemplo, es esencial para el diseño de productos financieros y la gestión de carteras de inversión. En la economía, permite analizar la dinámica de los mercados y estudiar las fluctuaciones de precios. Así, esta ecuación es una herramienta esencial para la ciencia y la tecnología modernas.
En la educación, la ecuación de Black-Scholes es un tema avanzado que se introduce en cursos de finanzas y economía. Los estudiantes aprenden a utilizarla para resolver problemas relacionados con la valoración de derivados. A medida que avanzan en sus estudios, descubren que esta ecuación es una herramienta poderosa que les permite comprender y modelar el comportamiento de los mercados financieros con mayor precisión. Se demuestra así como una de las ecuaciones históricas para el desarrollo de la ciencia económica.
Referencias:
- Whiteside, D. T. (2014). ‘And John Napier created logarithms...’ BSHM Bulletin: Journal of the British Society for the History of Mathematics, 29(3), 154–166. https://doi.org/10.1080/17498430.2014.874855
- Giraldo, J. G., & Malpica Vega, A. F. (2015). Un estudio introductorio a la ecuación de la onda en ℝⁿ.
- Rev. Bras. Ensino Fís. 30 (2) • 2008 • https://doi.org/10.1590/S1806-11172008000200012
- Martínez-Silíceo, M. F., Cruz-Reyes, L. F., Flores-Monroy, L. J., García-Novo, N. Y., & Reyes-Ángeles , T. (2022). Segunda Ley de la Termodinámica. TEPEXI Boletín Científico De La Escuela Superior Tepeji Del Río, 9(18), 48-51. https://doi.org/10.29057/estr.v9i18.8900




