Sabemos por experiencia que si lanzamos una pelota contra un muro, la pelota rebotará. Nunca vemos que atraviese la pared como un fantasma y aparezca al otro lado. Sin embargo, cuando realizamos un experimento semejante en el mundo microscópico, las cosas son diferentes. Por ejemplo, al lanzar electrones sobre barreras de energía microscópicas, en muchos casos, aunque la partícula no tenga energía para superar la barrera, a menudo sucede que la atraviesa limpiamente y aparece al otro lado.
Este es el «efecto túnel», una de las consecuencias más asombrosas de la mecánica cuántica. Recibe este nombre porque parece como si la barrera tuviera un agujero o túnel por donde pasara la partícula. Para discutir cómo tiene lugar, vamos a considerar un modelo simplificado, pero que capta todas las sutilezas del fenómeno. En este modelo la barrera está representada por una región con un potencial V. Esto es equivalente a una «montaña rectangular» con una cierta altura, de forma que la partícula necesita una energía V para superarla. Si lanzamos una partícula desde la izquierda con una energía menor, E < V, entonces la «intuición clásica» nos dice que no podrá superar la barrera, por lo que, al igual que la pelota anterior, rebotará.
Analicemos ahora el problema usando la mecánica cuántica. En primer lugar, hemos de describir el estado cuántico de la partícula que incide sobre la barrera. Una forma conveniente de hacerlo es mostrar la función de onda correspondiente. La función de onda de una partícula, ψ(x), toma un valor en cada punto (x) del espacio. Y ese valor (más exactamente su cuadrado, ψ(x)^2 nos proporciona la probabilidad de que, si medimos la posición de la partícula, la encontremos en dicho punto. ¿Cómo es la función de onda de nuestra partícula?
Nuestra hipótesis es que la partícula incidente posee una energía bien definida, E, menor que la altura energética de la barrera, E < V. Dado que para una partícula libre toda la energía es puramente cinética, la partícula tiene una velocidad bien definida. Según los postulados de la mecánica cuántica, la función de onda correspondiente tiene una forma parecida a una cuerda infinita agitada por una oscilación a lo largo de toda su longitud, como se muestra en la imagen.
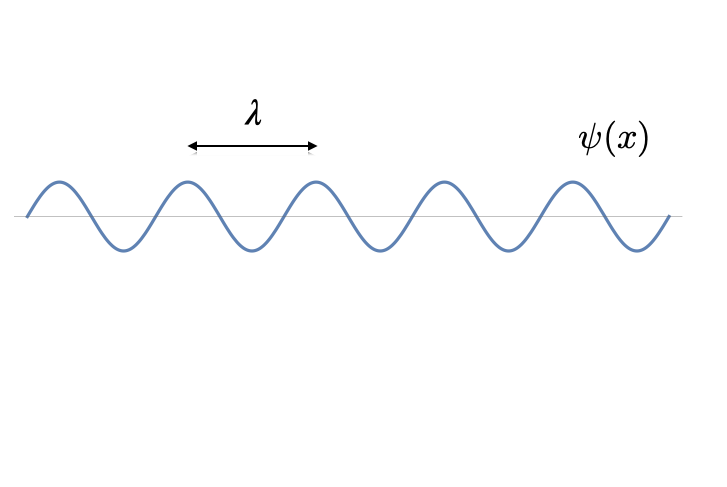
Una función así se denomina onda plana. Su característica más importante es la longitud de onda, o sea la distancia entre dos picos o dos valles. El valor de λ depende de la velocidad de la partícula: cuanto mayor sea esta, más pequeña es λ.
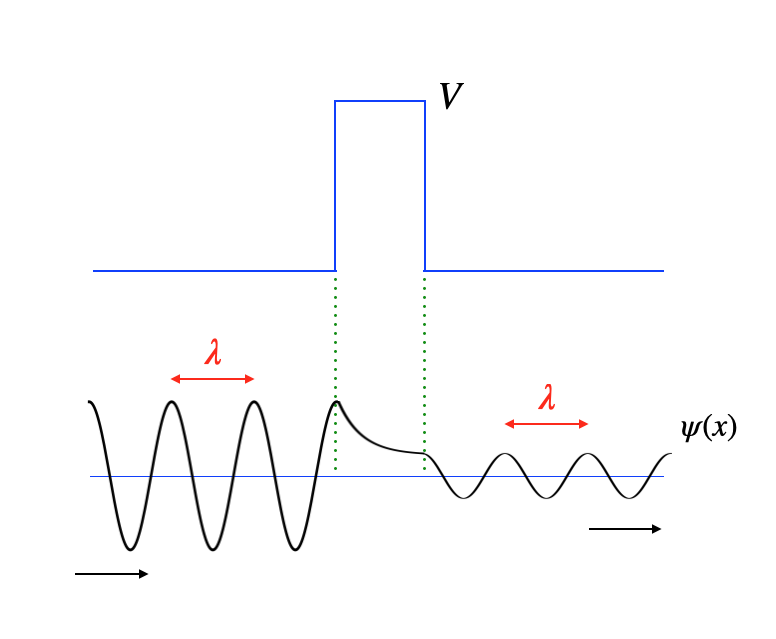
Si la intuición clásica fuera correcta, esta onda plana incidente debería reflejarse completamente en la barrera. Sin embargo, no es esto lo que sucede. Para estudiar la evolución de un sistema en mecánica cuántica se utiliza la llamada ecuación de Schrödinger, que describe cómo cambia con el tiempo la función de onda, ψ(x). Y cuando se aplica esta ecuación a la función de onda de nuestro problema se encuentra que, efectivamente, una parte de ella se refleja, pero no toda. La parte restante atraviesa la barrera y aparece al otro lado, como ilustra el diagrama.

Dado que el cuadrado de la función de onda, ψ(x)^2, proporciona la probabilidad de encontrar la partícula en un punto, la primera conclusión es que es posible detectarla a la derecha de la barrera, ya que ψ(x) es allí distinta de cero. De hecho, tiene una forma semejante a la función de onda incidente (una onda plana), pero con menor «amplitud de oscilación». Esto se debe a que solo una parte de la función de onda incidente se transmite, el resto se refleja. Sin embargo, la longitud de onda, λ, es la misma para la función de onda incidente y para la transmitida. Dado que la longitud de onda está relacionada con la velocidad de la partícula, la conclusión es que la velocidad de la partícula es igual a ambos lados de la barrera. En otras palabras, cuando la partícula lleva a cabo la hazaña de atravesar la muralla, lo hace «sin despeinarse», sin perder nada de su velocidad inicial.
Probabilidad de transmisión
La probabilidad de transmisión, es decir, de que se produzca este «mágico» efecto túnel, es mayor cuanto mayor sea la amplitud de la función de onda al otro lado de la barrera. Esa amplitud depende de forma muy sensible de la altura energética de la barrera, V, y de su anchura. Esto se debe a que dentro de la barrera la función de onda disminuye, y lo hace de forma exponencial.
Para situaciones microscópicas, en las que la altura y anchura de la barrera son pequeñas, la probabilidad de transmisión puede ser muy alta. Sin embargo, en situaciones cotidianas, donde las energías en juego y la anchura de las barreras son mucho mayores, la probabilidad de transmisión es ridículamente pequeña. Por tanto, aunque estuviéramos todo el tiempo lanzando pelotas contra la pared, tendría que pasar un número colosal de trillones de años, para que, con suerte, pudiéramos ver el fenómeno alguna vez. Sin embargo, en el mundo microscópico, lo observamos todos los días.
Todo lo anterior es lo que nos predice la mecánica cuántica. Y los experimentos se ajustan a la perfección a esas predicciones. Sin embargo, el sentido común parece indicarnos que hay algo contradictorio en todo este planteamiento. Podríamos pensar de la siguiente forma: «Si la partícula incidente aparece al otro lado de la barrera, es que en algún momento ha atravesado la zona del muro. Pero para estar en dicha zona se necesita como mínimo una energía igual al potencial del muro, E ≥ V. Esto parece contradecir nuestra hipótesis de partida de que la energía E es menor que V. Por tanto, la presencia de la partícula en la zona de la barrera debería estar prohibida en todo momento. Entonces, dado que la partícula no puede atravesar la zona de la barrera, tampoco debería poder acceder al otro lado de ella».

Hay que admitir que el hecho es, cuanto menos, sorprendente; sin embargo, a pesar de las apariencias, no hay contradicción lógica. El punto importante es tener claro qué significa la «probabilidad de presencia» en física cuántica. No es una medida de nuestra ignorancia. O sea, no es que la partícula esté «realmente» en algún punto pero nosotros ignoremos cuál es. Si fuera así, la partícula debería, efectivamente, pasar en algún momento por una zona prohibida energéticamente. Sin embargo, la partícula no tiene en ningún momento una posición definida, ya que su función de onda no está concentrada en un punto, sino extendida.
Extravagante para el sentido común
¿Qué significa entonces esa probabilidad de presencia no nula dentro de la barrera? Exactamente, que si medimos la posición de la partícula, hay una cierta probabilidad de que esta se materialice en esa zona. Es solo en ese momento cuando podríamos decir propiamente que la partícula está dentro de la barrera. Aun así, el hecho resulta paradójico. Al fin y al cabo, habríamos «cazado» a la partícula en el interior de la barrera, en flagrante violación de la conservación de la energía..., pero no hay tal violación. Lo que sucede en ese caso es que, en el proceso de medida, la partícula interactúa con el aparato de medición, de forma que se produce una transferencia de energía entre ellos; y ese aporte extra de energía es el que permite la materialización de la partícula en la zona de la barrera. Como sucede a menudo con la mecánica cuántica, la teoría parece jugar a violar principios muy arraigados, como el de la conservación de la energía, o incluso la pura lógica. Sin embargo, al final, no hay violación ni contradicción alguna, por más que la situación resulte extravagante para el «sentido común».
Es interesante mencionar que hay una relación directa entre el efecto túnel y el principio de incertidumbre. Este último nos dice que una partícula no puede tener bien definida la velocidad y la posición al mismo tiempo. Nuestra partícula posee una energía, y por tanto una velocidad, bien definidas. En consecuencia no puede tener bien definida la posición. De ahí que su función de onda esté extendida e incluso «penetre» en zonas prohibidas clásicamente, como el interior de la barrera.
Microscopio de efecto túnel
Para finalizar, discutamos el microscopio de efecto túnel, desarrollado en 1981 por los alemanes Gerd Binnig y Heinrich Rohrer, una de las aplicaciones más espectaculares de este fenómeno.
El microscopio está formado por una punta de un material conductor (tungsteno, platino- iridio u oro) extremadamente afilada. La punta se acerca al material que se quiere observar a una distancia de unas pocas diezmillonésimas de milímetro, apenas mayor que el tamaño de un átomo; lo cual, dicho sea de paso, requiere una mecánica extraordinariamente precisa. Entonces, entre la punta y el material estudiado se establece desde el exterior una diferencia de potencial. Si esta es muy grande, los electrones saltan espontáneamente desde la punta al material, se produce una chispa y se genera una corriente eléctrica en el circuito. Pero si disminuimos la diferencia de potencial, la atracción electrostática no es suficiente para que los electrones venzan la fuerza de ligadura que los mantiene unidos a los átomos del metal. En otras palabras: los electrones tendrían que atravesar una barrera energética, aparentemente insuperable, que se extiende entre la punta y el material.

Sin embargo, como hemos visto, la mecánica cuántica ofrece a los electrones una esperanza de superar esa barrera, gracias al efecto túnel. El número de electrones que lo consigue (y por tanto la magnitud de la corriente) depende de forma ultrasensible de la distancia entre la punta y el material. Pequeñísimas variaciones de esta se traducen en cambios sustanciales en la probabilidad de que los electrones superen la barrera, y, por consiguiente, en la corriente eléctrica que se establece.
A continuación, se «pasea» la punta sobre la muestra de material, con lo que la magnitud de la corriente va cambiando, dependiendo del relieve de su superficie. De esta manera, se cartografía ese relieve hasta límites de precisión extraordinarios. El resultado son unas imágenes con una resolución tan extrema que se observan perfectamente los átomos individuales del material.
No existe ningún instrumento de observación que se pueda comparar en resolución al microscopio de efecto túnel. A veces se dice que la mecánica cuántica es una teoría frustrante porque establece limitaciones a nuestro conocimiento sobre la naturaleza, aludiendo al principio de incertidumbre. Pero la realidad es que la mecánica cuántica no solo nos ha proporcionado un conocimiento muchísimo más profundo sobre cómo funciona la naturaleza, sino que nos ha permitido diseñar instrumentos para explorarla de forma más eficaz y precisa.
Este artículo se publicó en el número de coleccionista de Muy Interesante nº. 25, Mundo cuántico.




