En una clase de física, cuando sale el tema de la cuántica, alguien siempre pregunta: “¿Pero esto tiene sentido?”. Y la respuesta, con frecuencia, es una sonrisa incómoda del docente y una frase ya gastada: “La cuántica es así, no hay que entenderla, solo aceptarla”. La idea de que en el mundo subatómico rigen leyes que desafían la lógica cotidiana ha calado tan hondo que muchos la aceptan como una especie de dogma moderno: cosas que pasan y no se pueden explicar.
Pero, ¿y si sí se pudieran explicar? ¿Y si la extrañeza que sentimos frente a ciertos fenómenos cuánticos fuera solo un problema de perspectiva? En un artículo reciente, el físico argentino Alejandro Hnilo propone una forma distinta de ver varios de los experimentos más famosos de la cuántica. El paper, titulado "Quantum Mysteries Explained in Digestible Form", sugiere que muchos de los llamados “misterios” no son más que malentendidos lógicos derivados del uso inadecuado de conceptos matemáticos. Y para demostrarlo, recurre a una herramienta sorprendentemente accesible: la geometría euclidiana clásica.
Una reinterpretación desde la geometría
Uno de los mayores aportes de este trabajo es su forma de abordar la física cuántica sin recurrir al lenguaje matemático especializado que suele acompañar estos temas. En lugar de eso, Alejandro Hnilo usa vectores en un espacio tridimensional clásico, es decir, el mismo tipo de representaciones con las que se aprende geometría en el colegio. Este recurso le permite construir una visualización más clara e intuitiva de experimentos como los de Bell, Kochen-Specker o GHZ.
El núcleo de su enfoque está en cómo se representa una "proposición" cuántica. Hnilo sugiere que puede visualizarse como un vector cuya longitud tiene un significado físico y que puede superponerse con otros. La clave está en establecer cuándo ese vector es lo suficientemente largo como para que el sistema lo “acepte” como verdadero. Esto da lugar a una lógica condicional basada en umbrales, distinta de la lógica clásica booleana, en la que todo es blanco o negro.
Según el autor, “los fenómenos cuánticos pueden explicarse de modo sencillo si se reemplaza la lógica booleana por una lógica condicional basada en vectores”. De este modo, algunas de las paradojas cuánticas más famosas no serían tanto fenómenos extraños de la naturaleza, sino consecuencias de usar una lógica inadecuada para interpretarlos.
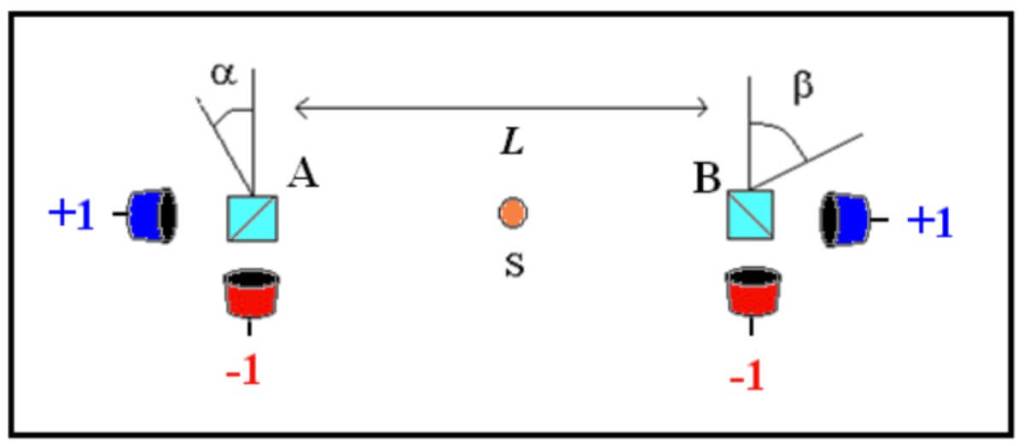
Bell, realismo y localidad: ¿una falsa dicotomía?
Uno de los debates más persistentes en física cuántica es si el mundo subatómico viola el realismo, la localidad, o ambas cosas. El realismo sostiene que las propiedades de las partículas existen aunque no se midan. La localidad implica que nada puede influir en otra cosa más rápido que la luz. Desde los años 60, con los experimentos inspirados en las desigualdades de Bell, muchos físicos han aceptado que la cuántica obliga a abandonar al menos una de estas ideas.
Pero Alejandro Hnilo ofrece una interpretación alternativa. Al modelar los resultados con su lógica de umbrales vectoriales, muestra que se puede reproducir la violación de las desigualdades de Bell sin renunciar al realismo ni a la localidad. Esto no es una refutación de la mecánica cuántica, sino una propuesta para entenderla desde otra lógica.
“Los resultados que comúnmente se interpretan como prueba de la no-localidad cuántica pueden explicarse como consecuencia de una lógica condicional no booleana”. Con esta frase, el autor plantea que el conflicto no está en los datos experimentales, sino en las suposiciones lógicas que usamos para analizarlos. Si se cambia el marco lógico, desaparece la necesidad de aceptar una física “misteriosa”.
Este enfoque no busca descartar la mecánica cuántica, sino reducir su misticismo. Según el autor, mucho de lo que hoy se considera “raro” o “no intuitivo” podría tener una explicación clara si usamos herramientas lógicas adecuadas al tipo de relaciones que describe el mundo cuántico.
GHZ y Kochen-Specker: nuevas formas de ver lo inexplicable
Uno de los puntos más interesantes del paper es la forma en que aborda el teorema GHZ, una extensión del experimento de Bell que plantea una contradicción aún más directa entre la lógica clásica y los resultados cuánticos. En el modelo de Hnilo, los vectores que representan proposiciones actúan como condiciones que deben superar ciertos umbrales. Al aplicar esta regla de decisión, la paradoja lógica que suele surgir en GHZ se disuelve.
Del mismo modo, el autor reformula el teorema de Kochen-Specker, que tradicionalmente se interpreta como una negación del realismo no contextual. En su enfoque vectorial, este tipo de contradicciones no se presentan porque las proposiciones no tienen valores de verdad fijos, sino condiciones contextuales que dependen del sistema en su conjunto. Esto cambia por completo el sentido de las conclusiones habituales en estos teoremas.
En el artículo se dice que “la interpretación tradicional de Kochen-Specker parte de supuestos lógicos que no aplican al modelo condicional propuesto”. Lo que propone Hnilo es una forma de salvar la coherencia lógica de la física sin necesidad de aceptar que la naturaleza es inherentemente paradójica.
Esta relectura tiene consecuencias no solo filosóficas, sino prácticas. Si los fenómenos cuánticos se pueden modelar sin romper el sentido común lógico, esto podría abrir nuevas vías para el diseño de tecnologías basadas en principios más accesibles y comprensibles.

Computadoras cuánticas desde otra lógica
Más allá de la interpretación conceptual, el paper también sugiere aplicaciones concretas. Una de las ideas más provocadoras es que esta lógica condicional basada en umbrales podría permitir el desarrollo de nuevas formas de computación cuántica, distintas de las actuales, que se basan en funciones de onda y operadores unitarios.
En vez de calcular probabilidades según la regla de Born, estas computadoras funcionarían con decisiones binarias condicionadas a si un vector supera o no cierto umbral. En otras palabras, podrían tomar decisiones cuánticas sin necesidad de medir amplitudes, sino simplemente evaluando condiciones vectoriales. “Esta lógica puede inspirar un nuevo tipo de computadora cuántica más cercana a estructuras geométricas que a la interferencia de amplitudes”.
Aunque se trata de una propuesta teórica, el valor está en que reduce el nivel de abstracción, acercando la computación cuántica a conceptos que podrían programarse de manera más directa, con ventajas potenciales en robustez y escalabilidad.
Esto no significa reemplazar los sistemas cuánticos actuales, sino explorar una vía distinta, en la que la geometría, más que la probabilidad, sea el motor del procesamiento de información.
¿Una física menos misteriosa?
El artículo de Alejandro Hnilo no niega los resultados de la mecánica cuántica ni cuestiona su validez empírica. Lo que hace es replantear su interpretación desde una lógica diferente, una lógica que permite explicar lo que sucede sin recurrir a fenómenos aparentemente mágicos ni a rupturas del sentido común.
Esto no es menor. La cuántica se ha convertido en sinónimo de lo incomprensible, lo indescifrable, lo “espeluznantemente no local”, como lo llamaba Einstein. Pero quizá parte de esa confusión proviene de usar herramientas lógicas pensadas para otro tipo de mundo. Si cambiamos esas herramientas, como propone este artículo, tal vez podamos ver los mismos resultados con otros ojos.
La propuesta es técnica, pero su impacto puede ser cultural: devolverle a la física cuántica una cuota de sentido. No es una negación del misterio, sino una invitación a reconsiderar qué parte de ese misterio es real y qué parte es solo nuestra forma de mirar.
Referencias
- Alejandro A. Hnilo. Quantum Mysteries Explained in Digestible Form. arXiv preprint. doi:10.48550/arXiv.2408.07779.




