Hay fenómenos en el universo que no necesitan exageraciones para resultar sobrecogedores. Los agujeros negros, por ejemplo, siguen siendo tan desconcertantes como fascinantes. Esos objetos que lo engullen todo —luz incluida— no solo deforman el espacio y el tiempo, sino que además vibran. Cuando un agujero negro es perturbado, como ocurre tras una fusión cósmica o al tragar materia, emite una especie de eco conocido como modo cuasinormal, una onda gravitacional que se disipa lentamente en el espacio. Esas vibraciones contienen información sobre su masa, su forma y su dinámica interna. Pero descifrarlas con precisión no ha sido tarea sencilla.
Un equipo de investigadores japoneses ha conseguido avanzar en este terreno utilizando una técnica matemática muy poco aplicada hasta ahora en física: el análisis exacto WKB (Wentzel-Kramers-Brillouin). Este método permite seguir con gran precisión cómo se propagan las ondas desde las cercanías del agujero negro hasta regiones lejanas del espacio. Su uso ha permitido detectar estructuras matemáticas complejas que antes se pasaban por alto, como curvas de Stokes que se enrollan en espiral. El resultado: un sistema que mejora notablemente el cálculo de las frecuencias más difíciles de captar, aquellas que se debilitan rápidamente.
Una vibración cósmica difícil de atrapar
Cuando un agujero negro se fusiona con otro o sufre alguna alteración, emite un "sonido" peculiar: una señal gravitacional que podemos detectar desde la Tierra con instrumentos como LIGO o Virgo. Esta señal tiene una fase final, conocida como ringdown o "repique", que contiene modos cuasinormales. Estos modos son claves para saber cómo es realmente el agujero negro.
El problema es que muchas de estas vibraciones se atenúan muy deprisa. Las más relevantes para los astrónomos, como las que nos hablan de agujeros recién formados o de los detalles más finos de su estructura, son precisamente las que resultan más difíciles de calcular con métodos teóricos tradicionales. Las aproximaciones numéricas funcionan, pero no siempre permiten captar el panorama completo.
Lo que propone el nuevo estudio es un enfoque que permite seguir matemáticamente el rastro de estas vibraciones débiles incluso cuando se vuelven casi indetectables. Para ello, el equipo recurrió al análisis exacto WKB, una técnica matemática usada sobre todo en contextos teóricos, pero muy poco explotada en la física de agujeros negros.

Qué es el método exacto WKB y por qué importa
El método WKB es una herramienta clásica que se usa para encontrar soluciones aproximadas a ecuaciones diferenciales en contextos donde varían de forma lenta. Su versión exacta, sin embargo, permite ir mucho más allá: consigue resumir de forma precisa una serie infinita de términos matemáticos divergentes, recuperando una solución coherente mediante un proceso llamado resumación de Borel.
Este procedimiento ha sido especialmente útil en contextos como la mecánica cuántica o ciertas teorías matemáticas. Pero su aplicación al estudio de agujeros negros no se había desarrollado en profundidad. Tal como explica el artículo, “aplicamos el análisis exacto WKB al cálculo de las frecuencias de los modos cuasinormales de los agujeros negros”.
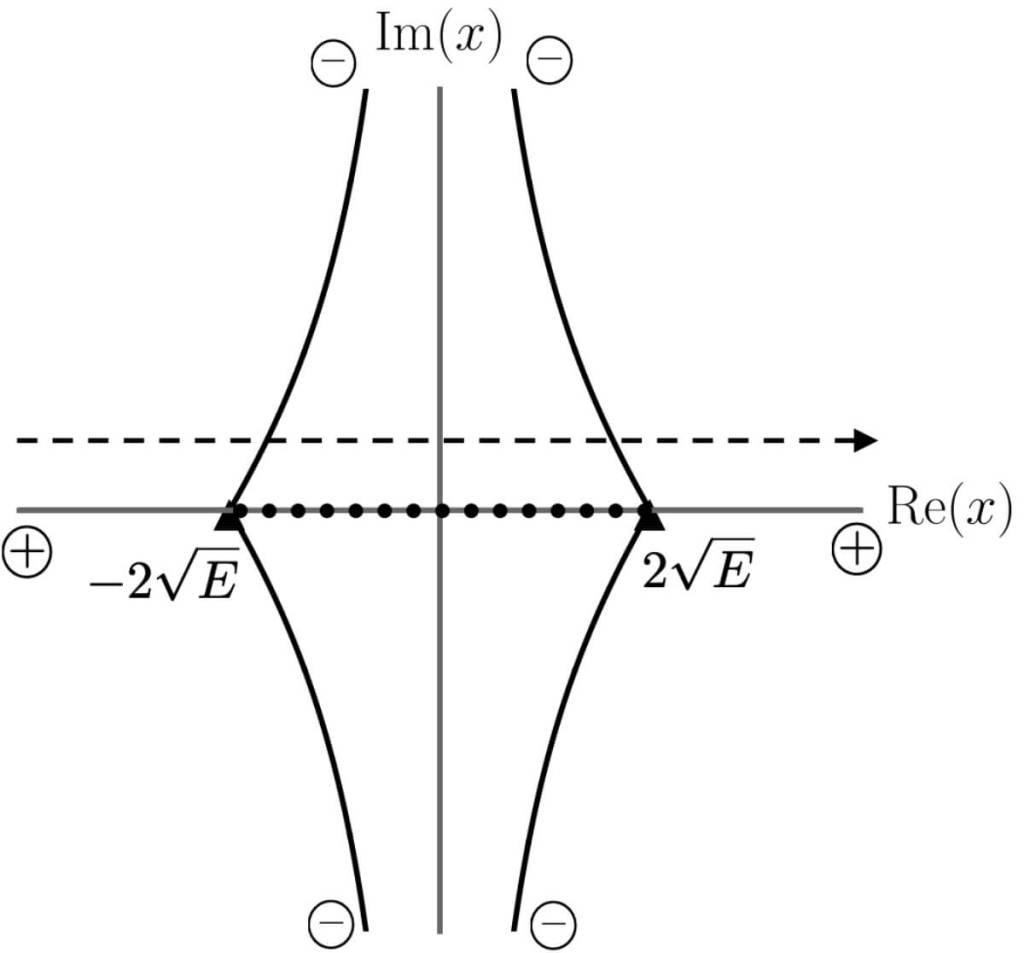
Gracias a esta herramienta, los autores pudieron describir con gran detalle la estructura global de las soluciones en el plano complejo, incluyendo efectos no triviales como las curvas de Stokes, que señalan regiones donde el comportamiento de las soluciones cambia de forma abrupta. Estas curvas, que a menudo se habían ignorado, resultaron esenciales para entender la física detrás del problema.

El hallazgo: curvas en espiral y estructuras ocultas
Uno de los descubrimientos más interesantes del estudio es la aparición de espirales logarítmicas en las curvas de Stokes, que surgen cerca de ciertos puntos singulares en el espacio-tiempo del agujero negro. Estas espirales no son meros detalles técnicos: su presencia afecta directamente a cómo se propagan las ondas y, por tanto, a cómo se detectan y analizan las vibraciones.
El análisis mostró que, al tener en cuenta esas curvas en espiral, el método WKB exacto lograba reproducir resultados correctos incluso en los casos más complejos, como el de las perturbaciones del espacio alrededor de un agujero negro de Schwarzschild. Según el artículo, “reformulamos cuidadosamente la derivación de las condiciones de los modos cuasinormales utilizando el análisis exacto WKB, incorporando estas características en el cálculo”.
Este enfoque no solo permite comprender cómo se comportan las vibraciones más débiles, sino que también mejora la conexión entre la teoría y los datos reales obtenidos por los detectores de ondas gravitacionales. En el futuro, podría contribuir a refinar la interpretación de señales procedentes de eventos cósmicos extremos.
Qué aporta frente a otros métodos
Existen otras formas de calcular los modos cuasinormales, como el método de la monodromía, que también emplea análisis en el plano complejo. Pero el nuevo estudio señala dos ventajas clave del método exacto WKB frente a la monodromía. Primero, este último impone ciertas aproximaciones antes del análisis, mientras que el WKB exacto permite hacer el desarrollo sin necesidad de aproximaciones hasta el final del proceso.
Segundo, el WKB exacto trabaja directamente sobre el eje real de coordenadas radiales, lo que simplifica el análisis y lo hace más compatible con los datos reales que manejan los astrofísicos. Esto resulta especialmente útil cuando se quiere estudiar la respuesta del espacio-tiempo a perturbaciones reales, como las que detectamos tras fusiones de agujeros negros.
El método también se puede extender fácilmente a otros tipos de agujeros negros, como los que rotan o los que tienen carga, e incluso a modelos que exploran posibles efectos cuánticos de la gravedad. Esto lo convierte en una herramienta muy versátil para la física teórica y la astrofísica.
Una nueva puerta hacia la geometría del universo
Este avance tiene implicaciones que van más allá de una mejora técnica. El estudio sugiere que, si se conocen con precisión los modos cuasinormales, se puede acceder a información más detallada sobre la geometría del espacio-tiempo que rodea a un agujero negro. Incluso podría ayudar a probar teorías que intentan unificar la relatividad general con la mecánica cuántica.
Los investigadores también afirman que su método podría aplicarse en contextos más amplios, como la cosmología o la teoría de cuerdas, donde las ecuaciones que gobiernan el comportamiento de ciertos sistemas son similares a las que describen las ondas en torno a un agujero negro. Como resultado, este enfoque podría aportar claridad en muchos frentes de la física actual.
A la espera de su aplicación en escenarios más complejos, como los agujeros negros en rotación, lo que queda claro es que este trabajo pone sobre la mesa una herramienta con gran potencial para futuras investigaciones. El hecho de que haya sido destacada como “Editor’s Suggestion” por la revista Physical Review D refuerza su relevancia dentro del campo.
Referencias
- Taiga Miyachi, Ryo Namba, Hidetoshi Omiya, Naritaka Oshita. Path to an exact WKB analysis of black hole quasinormal modes. Physical Review D. https://doi.org/10.1103/1gmr-9f1g.




