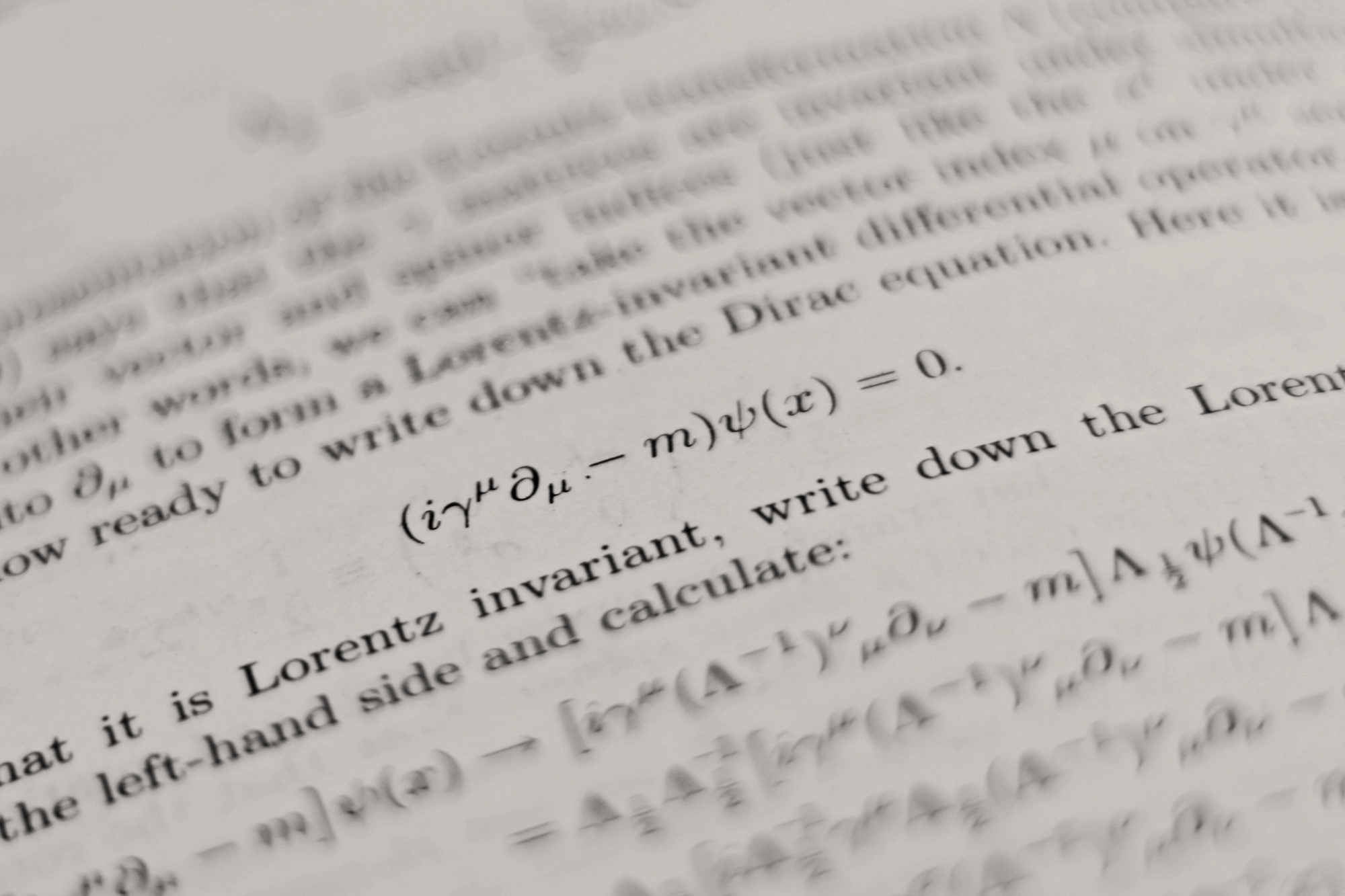En el tapiz infinitamente variado de la existencia humana, la belleza se entreteje en cada hilo. Tan etérea como omnipresente, escurridiza en su definición pero indudable en su presencia. La belleza se encuentra en crepúsculos serenos y en tormentas furiosas. En el brillo de una sonrisa genuina y en una risa compartida. En el baile de las hojas al viento y en la majestuosidad imperturbable de las montañas. Se encuentra en la sinfonía de una orquesta y en el silencio contemplativo de un museo, en la elegancia de un teorema matemático y en la precisión de un mecanismo ingenioso.
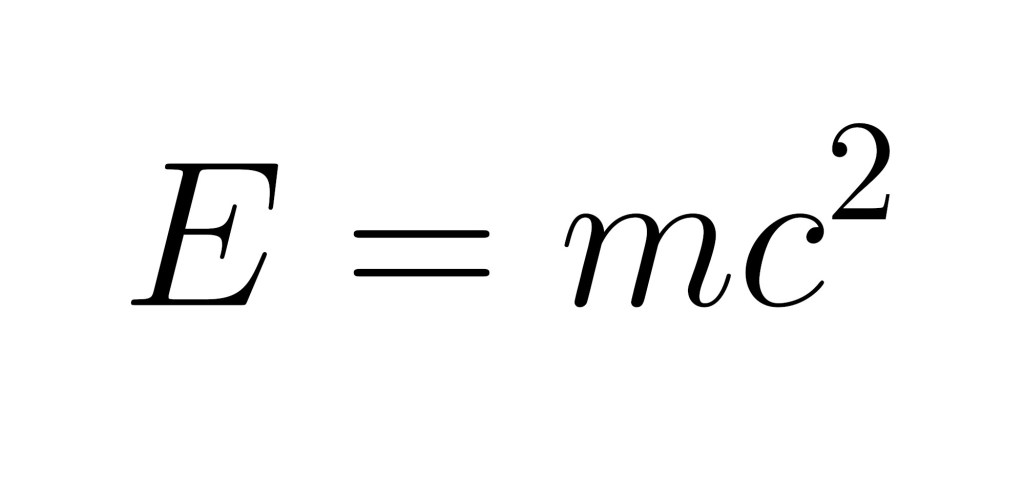
Dejaremos a otros autores hablar sobre otros tipos de belleza y aquí investigaremos la que podemos encontrar en las ecuaciones de la ciencia. La belleza de una ecuación puede entenderse desde varias perspectivas, todas entrelazadas con la naturaleza de cómo comprendemos el universo y los patrones subyacentes en él. La más evidente tal vez sea su simplicidad y elegancia. Una ecuación considerada bella suele tener una forma simple y concisa, pero al mismo tiempo, encerrar un significado profundo. Por ejemplo, E=mc2 de Einstein es breve y directa, pero encapsula en apenas unos símbolos la relación entre masa y energía que tiene implicaciones tan fundamentales para la radiactividad, el funcionamiento de las estrellas o la energía nuclear.

Una ecuación también puede resultar bella por su universalidad, por describir principios que son verdaderos o aplicables en una amplia variedad de situaciones. Las leyes de Newton del movimiento, por ejemplo, no solo se aplican a objetos en la Tierra sino también a cuerpos celestes, revelando un orden y coherencia en el universo. La segunda ley de Newton, que en su forma más simple se expresa como F=ma cumpliría este precepto. Esta ecuación nos dice que la acción de una fuerza F sobre un cuerpo de masa m provocará necesariamente una aceleración a. Esto es así independientemente de la naturaleza de la fuerza, que puede ser de contacto directo o de origen gravitatorio, eléctrico, elástico o debida por ejemplo a una diferencia de presión.

Otra fuente de belleza puede venir de la aparición de conexiones insospechadas. La identidad de Euler, aunque no sea estrictamente una ecuación, es especialmente bella. Esta identidad relaciona cinco cantidades fundamentales en matemáticas: i, la unidad imaginaria, la base de los números complejos; π, el número irracional por excelencia que entre otras cosas relaciona el radio y el perímetro de una circunferencia; e, la base de los logaritmos naturales y por último 0 y 1, las identidades de la suma y la multiplicación respectivamente.
Además de los motivos relativamente objetivos, también puede haber razones subjetivas para considerar bella una ecuación, o cualquier otra cosa cuya belleza se esté considerando. Son muchas las ecuaciones que se consideran bonitas en la física, por ejemplo, por la importancia histórica que tuvieron, por las implicaciones teóricas o por su poder de concretar toda una teoría en unos pocos símbolos.

Las ecuaciones del campo de Einstein, las ecuaciones fundamentales de la Relatividad General revolucionaron nuestra comprensión de la gravedad, mostrando que no es una fuerza a distancia, sino una consecuencia de la curvatura del espacio-tiempo causada por la masa y la energía. Cambiaron la forma en que entendemos el universo, abriendo el camino a conceptos como los agujeros negros y las ondas gravitacionales.
Las ecuaciones de Maxwell para el electromagnetismo unificaron por primera vez la electricidad, el magnetismo y la óptica en un solo marco teórico, revelando que la luz es una forma de radiación electromagnética. Además, pavimentaron el camino para la teoría de la relatividad de Einstein y han sido fundamentales en el desarrollo de innumerables tecnologías modernas.
El menos conocido Principio de Mínima Acción es una piedra angular en la física teórica, proporcionando un marco unificador para derivar las ecuaciones de movimiento de sistemas físicos. Desde la mecánica clásica hasta la teoría cuántica de campos, el principio de mínima acción ofrece un enfoque elegante y general para formular las leyes de la física, basado en la optimización de una cantidad (la acción). Su belleza radica en cómo una simple idea, que la naturaleza "elige" un camino que minimiza la acción, puede llevar a ecuaciones de movimiento complejas y precisas.

Sin embargo la que podríamos considerar como ecuación más bonita de toda la física es la que se conoce como ecuación de Dirac. Esta ecuación describe el comportamiento de los fermiones, partículas como electrones o quarks. Surgió del intento de Paul Dirac de conciliar la mecánica cuántica con la teoría especial de la relatividad de Einstein. Mientras la ecuación de Schrödinger funcionaba bien para describir partículas a velocidades mucho menores que la velocidad de la luz, fallaba al incorporar los efectos relativistas. Dirac buscaba una ecuación que pudiera describir correctamente el comportamiento de las partículas a altas velocidades y que por tanto respetara los principios de la relatividad.
Uno de los logros más sorprendentes de la ecuación de Dirac fue su predicción de la existencia de antimateria, una idea revolucionaria en aquel momento. La ecuación implicaba la existencia de partículas con la misma masa que las partículas conocidas, pero con cargas opuestas. Esta predicción fue confirmada experimentalmente con el descubrimiento del positrón en 1932, una partícula con la misma masa que el electrón pero con carga eléctrica positiva, lo que supuso un triunfo espectacular para la teoría. A pesar de la complejidad de los fenómenos que describe, la ecuación de Dirac es notablemente simple y elegante. Utiliza los "espinores" y las matrices de Dirac para formular una ecuación que es lineal en derivadas tanto temporales como espaciales, una forma que es tanto matemáticamente atractiva como práctica.
Referencias:
- Griffiths, David J. (2008). Introduction to Elementary Particles (Second, Revised ed.). Wiley-VCH. ISBN 978-3-527-40601-2
- An Introduction to Quantum Field Theory, M. Peskin, and D. Schroeder. Westview Press, (1995) ISBN 9780813345437