Durante siglos, resolver ecuaciones polinómicas de quinto grado o superiores fue considerado un callejón sin salida en las matemáticas. Desde que Évariste Galois demostrara en 1832 que no existía una fórmula general en radicales para resolverlas, la comunidad matemática aceptó esa barrera como definitiva. Hoy, un nuevo enfoque sacude esa certidumbre. Norman Wildberger y Dean Rubine han propuesto una solución radicalmente distinta: una serie infinita de términos basada en una generalización de los números de Catalan, que permite resolver este tipo de ecuaciones desde un enfoque puramente algebraico y combinatorio.
El artículo, publicado en abril de 2025 en la revista The American Mathematical Monthly, ofrece una fórmula que evita por completo el uso de raíces cuadradas, cúbicas o de orden superior, que históricamente complicaban la resolución de estas ecuaciones. En su lugar, los autores recurren a una estructura geométrica y combinatoria basada en subdivisiones de polígonos: los llamados subdigones. Así, logran construir una serie formal infinita que, al truncarse, puede dar soluciones aproximadas con gran precisión. Pero, más allá de la técnica, lo que esta propuesta plantea es un rediseño conceptual sobre qué significa "resolver" una ecuación algebraica.
Una barrera histórica, un cambio de perspectiva
Durante más de 150 años, la teoría de Galois marcó un límite claro para el álgebra: no se podía encontrar una solución general para polinomios de grado cinco o más utilizando radicales. Ese resultado, aunque matemáticamente riguroso, enclavó la cuestión en el terreno de lo irresoluble. Lo que Wildberger y Rubine proponen no contradice esa conclusión, sino que cambia las reglas del juego.
Según explican en el paper, su propuesta "reconsidera lo que realmente significa resolver una ecuación algebraica". En lugar de intentar encontrar una fórmula cerrada basada en raíces, como las del tipo raíz cuadrada o cúbica, construyen una solución en forma de serie infinita de términos combinatorios. Esta serie, por su forma y estructura, no necesita recurrir a los irracionales ni a operaciones infinitas tradicionales, lo cual evita las críticas filosóficas y técnicas que Wildberger lleva tiempo formulando contra el uso de números como raíz de dos o raíz cúbica de siete.

Catalan como puerta de entrada
Los números de Catalan aparecen en muchos contextos matemáticos: conteo de expresiones bien formadas, caminos en rejillas, particiones de conjuntos… y, como descubren los autores, también como solución formal a ciertas ecuaciones cuadráticas. En concreto, la ecuación 1 - α + tα² = 0 tiene como solución formal la serie generadora de los números de Catalan, sin necesidad de aplicar la fórmula cuadrática clásica.
Esta conexión no es decorativa. "La ecuación 1 - α + tα² = 0 tiene una solución en serie formal: α = T[t], donde T[t] = suma de Cn·tⁿ", explican literalmente los autores. Esta construcción se convierte en un modelo para abordar ecuaciones de grados más altos. A partir de ahí, la generalización es natural: extender la estructura combinatoria de los números de Catalan a otros casos más complejos.
¿Qué significa exactamente esta expresión? Que, en lugar de buscar una única solución con raíces cuadradas, lo que se hace es construir una suma infinita de términos, cada uno con un peso determinado por los números de Catalan. Cada término representa una especie de "paso" hacia la solución, y está formado por una constante combinatoria multiplicada por una potencia de una variable auxiliar. Al sumar todos estos términos, se obtiene una representación de la solución mucho más flexible: no se necesita calcular infinitos decimales ni aceptar irracionales, sino solo sumar hasta donde sea necesario para lograr la precisión deseada.
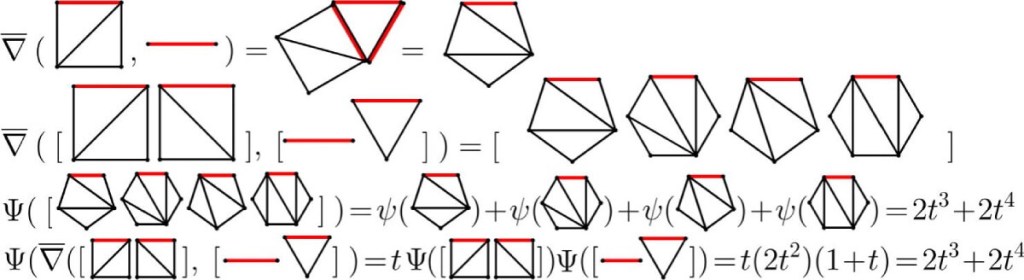
La invención de los subdigones y los números hiper-Catalan
Para ampliar el enfoque a polinomios de cualquier grado, los autores introducen los subdigones: polígonos con una arista marcada que se dividen en figuras como triángulos, cuadriláteros o pentágonos mediante líneas internas que no se cruzan. Cada subdivisión tiene un tipo, definido por un vector m = [m2, m3, m4, ...], donde m2 representa el número de triángulos, m3 el de cuadriláteros, y así sucesivamente.
Con esta estructura, definen los números hiper-Catalan, que generalizan los Catalan clásicos. "Definimos el número hiper-Catalan Cm como el número de subdigones de tipo m", declaran. Estos números permiten organizar los términos de una serie formal multivariable, cada uno correspondiente a una forma específica de subdividir un polígono.
El resultado no es una simple curiosidad combinatoria: esta serie se convierte en la base para resolver cualquier ecuación polinómica. No mediante raíces o símbolos irracionales, sino por un desarrollo ordenado y truncable de términos algebraicos perfectamente definidos.

Una fórmula para todos los polinomios
La clave del artículo es la presentación de una fórmula general que, teóricamente, sirve para resolver cualquier ecuación polinómica de una variable, sea cual sea su grado. Esta fórmula se expresa como una suma infinita, donde cada término está compuesto por un número hiper-Catalan, potencias de los coeficientes del polinomio y divisiones por factores derivados de la estructura del subdigón correspondiente.
El resultado es elegante y potente: “La ecuación 0 = c0 − c1x + c2x2 + c3x3 + … tiene una solución formal dada por x = suma sobre m de x = Σₘ Cm · c0Vm-1 · cm / c1Em.
Vaya lío. Veamos...
Aquí, Cₘ es un número que cuenta cuántas formas hay de construir una figura poligonal (un “subdigón”) de cierto tipo. Vₘ indica cuántos vértices tiene esa figura, y Eₘ cuántos lados o aristas. Por su parte, cₘ es una combinación de varios de los coeficientes del polinomio original (como c₂, c₃, etc.), elevados a potencias según la forma concreta del subdigón. Aunque todo esto suene muy técnico, lo importante es que cada pieza de la fórmula representa algo concreto y bien definido, y que esta suma infinita se puede cortar en cualquier punto para obtener una aproximación útil y precisa a la solución del polinomio.

Aplicaciones prácticas y ejemplos
Los autores ponen a prueba su método con un caso clásico: la ecuación cúbica x³ - 2x - 5 = 0, usada históricamente para ilustrar el método de Newton. Aplicando los primeros términos de su serie, logran una aproximación bastante precisa. Luego, refinan el resultado mediante un proceso iterativo al que llaman bootstrapping, y con apenas unos pasos adicionales, alcanzan una precisión superior a las cuatro cifras decimales.
Este enfoque no solo es original, sino también práctico. Permite crear programas informáticos que resuelvan polinomios sin depender de funciones irracionales ni algoritmos de aproximación clásicos, lo que puede tener implicaciones en campos tan diversos como el diseño de algoritmos, la computación simbólica o la resolución de ecuaciones en sistemas discretos.
El Geode: una nueva capa estructural
Una de las sorpresas del artículo es la aparición del Geode, una matriz de números que organiza y da forma interna a la serie hiper-Catalan. Su nombre refleja una idea central: dentro de la serie hay una estructura más profunda que parecía oculta, pero que puede factorizarse de forma precisa.
Los autores no ocultan su entusiasmo: "Introducimos esta matriz fundamentalmente nueva, el Geode, que extiende los números de Catalan clásicos y parece subyacer a ellos". Aunque todavía no hay una fórmula cerrada general para el Geode, se han identificado formas parciales, como su versión Bi-Tri, donde se cuenta el número de subdigones con m2 triángulos y m3 cuadriláteros.
El Geode no solo ayuda a organizar la serie: podría revelar propiedades combinatorias universales que van más allá del álgebra. Su estudio abre una línea de investigación completamente nueva, con potencial impacto en teoría de árboles, estructuras de datos y geometría algebraica.
Referencias
- N. J. Wildberger & Dean Rubine (2025): A Hyper-Catalan Series Solution to Polynomial Equations, and the Geode, The American Mathematical Monthly, DOI: 10.1080/00029890.2025.2460966.